| 23 四角柱・四角すい (略解) | ||
| 23 四角柱・四角すい (略解) | ||
| 1 | 法政大国際高校 (R4年) ★★★ | 4 | 広島大附属高校 (R4年) ★★★ | |||||||||||||||||||||||||||||
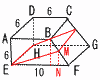 四角形AEFBを底面,辺DAを高さとみなした四角柱AEFB-DHGCである。 四角形AEFBを底面,辺DAを高さとみなした四角柱AEFB-DHGCである。(1) この四角柱の体積を求めよ。 【解】体積=底面積×高さの4辺の平均より,
(2) 線分MNの長さを求めよ。 【解】6△EFM=288× (3) 切り口の面積を求めよ。 【解】FN:4= △MENで, ME2=( ME= |
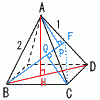 (1) 正四角すいABCDEの体積 (1) 正四角すいABCDEの体積【解】△ABHは直角二等辺三角形 △ABHで,AH=BH=√2 体積= (2) 線分APの長さ 【解】△ABDは直角二等辺三角形 △ABFで,BF=√22+12=√5 △ABF= 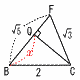 (3) 線分CQの長さ (3) 線分CQの長さ【解】△CBFで,BQ=xとすると, CQ2=22−x2=(√3)2−(√5−x)2 これを解いて,x= CQ=√ { 4−( |
|||||||||||||||||||||||||||||||
| 2 | 秋田県立高校 (R5年) ★★ | 5 | 大阪星光学院高校 (R4年) ★★★ | |||||||||||||||||||||||||||||
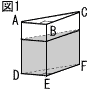 図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。 図1のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB=6cm,BC=8cm,CF=12cm,∠ABC=90°である。図2のように,四角形FEBCが容器の底になるように,水平な台 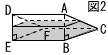 の上に置きかえたとき,容器の底から水面までの高さを求めなさい。 の上に置きかえたとき,容器の底から水面までの高さを求めなさい。【解】(右下図参照)
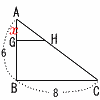 図2の△ABCで,AG=xとすると, 図2の△ABCで,AG=xとすると,体積比より,次のようになればよい △AGH:△ABC=x2:62=1:3 x2=36÷3=12で,x=2√3 GB=(6−2√3)cm |
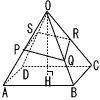 (1) OH=[ ], OI=[ ] (1) OH=[ ], OI=[ ]【解】対角線AC=6√2 △OAHで,OH=√62−(3√2)2=3√2 PR‖ACより,OI= (2) ∠DOB=[ ]度, OS=[ ], △OSQ=[ ] 【解】△DOBは直角二等辺三角形で,∠DOB=90度
(3) 四角すいO-PQRSの体積は[ ]である。 【解】垂直に2分割して考える 正四角錐O-ABCDの体積V= 三角錐O-PQR=18√2× 三角錐O-PSR=18√2× ア+イより, 体積=3√2+ |
|||||||||||||||||||||||||||||||
| 3 | 桐朋高校 (R6年) ★★★ | 6 | 法政大国際高校 (R6年) ★★★ | |||||||||||||||||||||||||||||
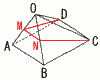 AB=1である長方形ABCDを底面とする四角錐O-ABCDで, AB=1である長方形ABCDを底面とする四角錐O-ABCDで,(1) △OBCの面積を求めよ。 【解】OB=OC=AD=√2で,△OBCは正三角形 △OBC= (2) 四角錐O-ABCDの体積を求めよ。 【解】∠OAB=∠DAB=90°より,高さ= 体積= (3) このとき,点Oを含む方の立体の体積を求めよ。 【解】MN⊥△OAD △OMDを底面とする切頭三角柱と考える △OMD=
|
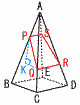 (1) 四角錐A-BCDEの表面積を求めよ。 (1) 四角錐A-BCDEの表面積を求めよ。【解】側面の高さ=√122−32=3√15 表面積=( (2) 四角錐A-BCDEの体積を求めよ。 【解】△ABDの高さ=√ { 122−(3√2)2}=3√14 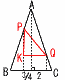 体積= 体積=(3) このとき,四角形PQRSの面積を求めよ。 【解】 △PQKで,PK=3√15×( QK= 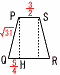 PQ=√ { ( PQ=√ { (△PQHで,PH=√ { (√31)2−( |
|||||||||||||||||||||||||||||||