 図形 |
２３ 四角柱・四角すい | 月 日（ ） |
| 図形 |
２３ 四角柱・四角すい | 月 日（ ） |
| １ | 法政大国際高校 （Ｒ４年） ★★★ | ４ | 広島大附属高校 （Ｒ４年） ★★★ |
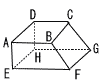 図は,四角形AEFBを底面,辺DAを高さとみなした四角柱AEFB-DHGCでＢある。AB//EF,AE⊥AB,AB＝AE＝AD＝6,EF＝10であるとき,(1) この四角柱の体積を求めよ。 (2) 点Eと点Ｈを通り,四角柱AEFB-DHGCの体積を2等分する平面をPとする。平面Pと辺BFとの交点をMとし,点Mから辺EFに下ろした垂線と辺EFとの交点をNとする。このとき,線分MNの長さを求めよ。 (3) (2)において,四角柱を2等分したときの切り口の面積を求めよ。 |
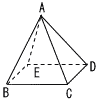 図は,すべての辺の長さが2cmで,底面が正方形BCDEの正四角すいABCDEである。辺ADにAF＝1cmとなるように点Fをとり,点Aから線分BFにひいた垂線と線分BFとの交点を点P,点Cから線分BFにひいた垂線と線分BFとの交点を点Qとする。(1) 正四角すいABCDEの体積を求めよ。 (2) 線分APの長さを求めよ。 (3) 線分CQの長さを求めよ。 |
||
| ２ | 秋田県立高校 （Ｒ５年） ★★ | ５ | 大阪星光学院高校 （Ｒ４年） ★★★ |
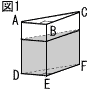 図１のように,三角柱ABC-DEFの形をした透明な容器に,水を入れて密閉した。この容器の側面はすべて長方形で,AB＝6cm,BC＝8cm,CF＝12cm,∠ABC＝90°である。この容器を,△DEFが容器の底になるように,水平な台の上に置いた。このとき,容器の底から水面までの高さは8cmである。 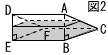 この容器を図2のように,四角形FEBCが容器の底になるように,水平な台の上に置きかえたとき,容器の底から水面までの高さを求めなさい。ただし,容器の厚みは考えないものとする。 |
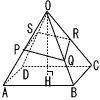 図のように,すべての辺の長さが6の正四角すいO-ABCDがある。辺OAの中点をP,辺OBの三等分点のうちBに近い方の点をQ,辺OCの中点をRとし,3点P,Q,Hを通る平面と辺ODとの交点をSとする。またOから平面ABCDに下ろした垂線をOHとし,OHと平面PQRSとの交点をIとする。(1) OHの長さは[ ]であり,OIの長さは[ ]である。 (2) ∠DOB＝[ ]度で,OSの長さは[ ]であるから,△OSQの面積は[ ]である。 (3) 四角すいO-PQRSの体積は[ ]である。 |
||
| ３ | 桐朋高校 （Ｒ６年） ★★★ | ６ | 法政大国際高校 （Ｒ６年） ★★★ |
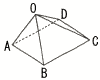 AB＝1である長方形ABCDを底面とする四角錐O-ABCDで,OA＝AB,CD＝CD,∠OAB＝∠ODC＝∠AOD＝90°とする。(1) △OBCの面積を求めよ。 (2) 四角錐O-ABCDの体積を求めよ。 (3) 辺OAの中点をMとし,3点M,C,Dを通る平面で四角錐O-ABCDを切る。このとき,点Oを含む方の立体の体積を求めよ。 |
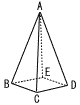 図のような正四角錐A-BCDEがある。AB＝AC＝AD＝AE＝12,正方形BCDEの1辺の長さが6であるとき,(1) 四角錐A-BCDEの表面積を求めよ。 (2) 四角錐A-BCDEの体積を求めよ。 (3) 辺AB,AC,AD,AE上に,それぞれ点P,Q,R,Sを,AP:PB＝1:3,AQ:QC＝2:1,AR:RD＝2:1,AS:SE＝1:3となるようにとる。このとき,四角形PQRSの面積を求めよ。 |
||
