 図形 |
２５ 円柱・円すい （略解） | |
| 図形 |
２５ 円柱・円すい （略解） | |
| １ | 芝浦工大附属高校 （Ｒ６年） ★ | ５ | 静岡県立高校 （Ｒ５年） ★★ | |||||||
 右の図のように,母線の長さが10cmの円すいを平面上ですべらないように転がしたところ,ちょうど5回転してもとの位置に戻った。このとき,円すいの表面積を求めなさい。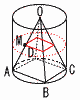 【解】円錐の底面半径をrとすると,移動円周＝2r×5＝20πで,r＝2 表面積＝  ×4π×10＋22π＝24πcm2 |
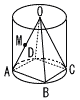
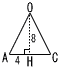
 △ODFの面積を求めなさい。 【解】AO＝√62−32＝3√3 △DOEで,DO2＝(  √3)2＋()2より,DO(等辺)＝3 △DFEで,DF2＝( √3)2＋(√3)2より,DF(底辺)＝ √6△ODFは二等辺三角形で,高さは  √10よって, ×(√6)×(√10)＝ √15cm2 |
|||||||||
| ２ | 法政大高校 （Ｒ４年） ★ | ６ | 桃山学院高校 （Ｒ６年） ★ | |||||||
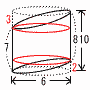 図は,円柱を2つの平面で切断してできた立体である。この円立体の体積を求めなさい。【解】右図参照 体積＝32π(3× ＋5＋2×)＝9π×  ＝(135/2)π【別解】切頭円柱＝底面積×高さの平均
|
 右の図の立体Aは,半径が3cmの半球と底面の半径が3cmで母線の長さが5cmの円すいを合わせたものです。また,立体Bは底面の半径が3cmの円柱です。立体Aと立体Bの体積が等しくなるときの立体Bの高さを求めなさい。【解】Bの高さをhとすると, B＝32π×h＝9πh …ア A＝  π×33÷2＋ ×32π×5＝33π…イア＝イより,9πh＝33πで, h＝  cm |
|||||||||
| ３ | 日本大習志野高校 （Ｒ６年） ★★ | ７ | 茨城県立高校 （Ｒ４年） ★★★ | |||||||
 右図のように底面の半径が6cm,高さが8cmの円錐Aがあり,底面は平面P上にある。円錐Ａを右図のように,平面P上を12cm移動させる。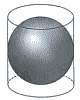 (1) 円錐Aの側面の展開図であるおうぎ形の中心角の大きさを求めなさい。【解】母線＝√62＋82＝10cm 中心角をxとすると, 扇形の弧＝20π×  ＝12πで, x＝216°(2) 図のように移動させたとき,円錐Ａが通過した部分の立体について,体積と表面積をそれぞれ求めなさい。 【解】立体は上図の円錐(アウ)＋三角柱(イ) 体積＝ ×62π×8＋(×12×8)×12＝(96π＋576)cm3円錐の表面積＝ ×12π×10＋62π＝96π三角柱の側面積＝(10＋10＋12)×12＝384 表面積＝(96π＋384)cm2 |
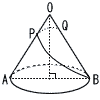 図のような,底面の半径が2cm,母線の長さが6cm,高さが4√2cm,頂点がOの円すいがある。(1) この円すいの体積を求めなさい。 【解】 体積＝ ×22π×4√2＝ √2πcm3(2) この円すいの表面績を求めなさい。 【解】 面積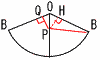＝ ×4π×6＋22π＝12π＋4π＝16πcm2 (3) ひもの長さが最短となるように点Qをとるとき,そのひもの長さを求めなさい。 【解】展開図(120°の扇形)で考える OP＝2より,PQ＝PH＝√3, OH＝1 △PBHで,PB＝√(√3)2＋(6−1)2＝2√7 長さ＝PQ＋PB＝(√3＋2√7)cm |
|||||||||
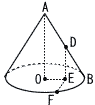
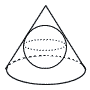
| ４ | 東北学院高校 （Ｒ６年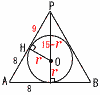） ★★ |  (2) 球Oの半径を求めなさい。【解】球の半径をrとすると, △POHで,r2＋92＝(15−r)2 これを解いて,r＝  |
||||||||
 右の図のような,球Oがちょうど入る円錐の容器があります。円錐の底面の半径が8cm,高さが15cmのとき,(1) この円錐の表面積を求めなさい。 【解】母線＝√82＋152＝17cm 表面積＝ ×16π×17＋82π＝200πcm2 |
||||||||||