 図形 |
２６ 切断と切り口 （略解） | |
| 図形 |
２６ 切断と切り口 （略解） | |
| １ | 大阪教育大附属平野校舎高校 （Ｒ５年） ★ | ４ | お茶の水女子大附属高校 （Ｒ５年） ★★★ |
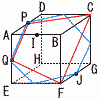 １辺の長さが4cmの立方体ABCD-EFGHがある。辺AB,FG,AD,AEの中点をそれぞれI,J,P,Qとする。次の3点を通る平面でこの立方体を切断するとき,切り口の形と切り口の周の長さを答えなさい。(1) P,Q,I 【解】△PQI 正三角形 2√2×3＝6√2cm (2) P,Q,F 【解】  PQFC(右上の赤図)台形 2√2＋2√5×2＋4√2＝(6√2＋4√5)cm (3) P,Q,J 【解】(右上の青図) 正六角形 2√2×6＝12√2cm |
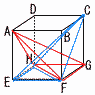 図のような１辺の長さが1の立方体ABCD-EFGHがある。4点A,F,G,Hを頂点とする三角すいSと,4点C,F,E,Hを頂点とする三角すいＴがあるとき,(1) 三角すいSの表面積を求めなさい。 【解】△FGH＋△AFG＋△AHG＋△AHF S＝  ＋ ×2＋ ＝ ＋√2＋ (2) 辺AE上にAP:PE＝m:nとなるような点Pをとり,点Pを通り底面EFGHに平行な平 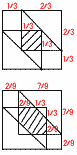 面でこの2つの三角すいS,Tを切ったとき,2つの立体SとTの切り口の図形が重なった部分の面積をMとする。① m:n＝2:1のときのMの値を求めなさい。 【解】正方形 M＝(  )2＝ ② m:n＝7:2のときのMの値を求めなさい。 【解】正方形＋長方形 M＝(  )2＋√2×√2＝16/81 |
||
| ２ | 明大中野八王子高校 （Ｒ４年） ★★ | ５ | 須磨学園高校 （Ｒ４年） ★★ |
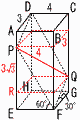 図のように,AD＝3cm,CD＝4cmの直方体ABCD-EFGHを平面DPFQで切ると,∠PFE＝60°,∠QFG＝30°となるとき,(1) 平行四辺形DPFQの対角線PQの長さを求めなさい。 【解】（右図参照） △APDで,AP＝√3,△PEFで,PE＝4√3 PR＝PE－AP＝4√3－√3＝3√3 PQ＝√32＋42＋(3√3)2＝√52＝2√13 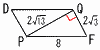 (2) 平行四辺形DPFQの面積を求めなさい。【解】QF＝2√3 PQ2＋QF2＝PF2より,△PQFは直角三角形 DPFQ＝2△PDF＝2√13×2√3＝4√39cm2 |
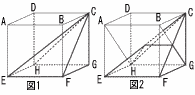 4辺AE,BF,CG,DHのそれぞれの中点を通る平面で切断する。(1) VとWの比を,最も簡単な整数比で表しなさい。 【解】V:(V＋W)＝12:22＝1:8 V:W＝1:(8－1)＝1:7 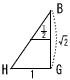 (2) 切断面の面積を求めなさい。 【解】切断面は台形 面積＝ (＋1)×√2＝ √2(3) 点Cを含む立体の体積を求めなさい。 【解】 体積＝ × √2×√2＝ |
||
| ３ | 土浦日本大高校 （Ｒ６年） ★ | ６ | ラ・サール高校 （Ｒ６年） ★★★ |
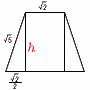 図は1辺の長さが2の立方体ABCD-EFGHである。辺BC,辺CDの中点をそれぞれM,Nとし,4点M,N,H,Fを通る平面でこの立方体を切り分けたとき,(1) 【解】MN＝[ √2 ], MF＝[ √5 ] (2) 四角形MNHFの面積は[ ]である． 【解】 MNHFは等脚台形ｈ＝√ { (√5)2－( )2}＝ √2面積＝ ×(√2＋2√2)×√2＝ (3) 切り分けた立体のうち,点Cを含む側の立体の体積は[ ]である。 【解】水平に半分に切断した三角錐台 体積＝ ×(×22)×4× ＝ |
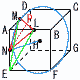 立方体のすべての辺に接する球Oをとるとき,(1) 球Oの半径を求めよ． 【解】対称面AEBCで考える 半径＝ON＝2√2× 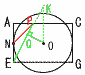＝√2 (2) 3点,L,M,Nを通る平面で球Oを切ったときの切り口の面積を求めよ。【解】切り口は△LMN(1辺√2)の外接円 半径＝ √6で, 面積＝(√6)2π＝ π(3) 3点L,M,Eを通る平面で球Oを切ったときの切り口の面積を求めよ。 【解】半径OQを求める OK＝3で,△AEP∽△QKO(相似比1:√2) OQ＝√2APで,OQ＝√2× ＝1面積＝12π＝π |
||