| �Q�V�@��]�́@�i�����j | ||
| �Q�V�@��]�́@�i�����j | ||
| �P | �������Z�@�i�q�S�N�j�@�� | �S | ��ʌ������Z�@�i�q�U�N�j�@�� | ||||||||||||||||||||||||
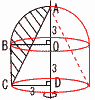 �@�ΐ�������,����AD�����Ƃ���1��]�����Ăł��闧�̂̑̐ς����߂�B �@�ΐ�������,����AD�����Ƃ���1��]�����Ăł��闧�̂̑̐ς����߂�B�y���z�����{�~���|�~�� �@��18���{27���|18����27�� |
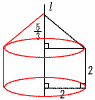 �@�E�̐}�̂悤��AB��AC��2cm,��BAC��90���́�ABC������,���_C��ʂ�,��BC�ɐ����Ȓ���/���Ђ��܂��B���̂Ƃ�,��ABC��,����/�����Ƃ���1��]�����Ăł��闧�̂̑̐ς����߂Ȃ����B �@�E�̐}�̂悤��AB��AC��2cm,��BAC��90���́�ABC������,���_C��ʂ�,��BC�ɐ����Ȓ���/���Ђ��܂��B���̂Ƃ�,��ABC��,����/�����Ƃ���1��]�����Ăł��闧�̂̑̐ς����߂Ȃ����B�y���z��~���|���~���~2 �̐ρ� |
||||||||||||||||||||||||||
| �Q | ����{�������w�@�@�i�q�T�N�j�@������ | �T | ���卂���w�@�@�i�q�S�N�j�@������ | ||||||||||||||||||||||||
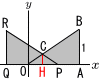 �@���_��0�Ƃ�����W���ʏ�ɓ_A(��3,0), B(��3,1)������B0��t����3�ɑ���,P(t,0), Q(t�|��3,0), R(t�|��3,1)���Ƃ�B����PR�ƒ���OB�̌�_��C�Ƃ���B5�̐����ň͂܂�镔���̐}�`��,x�������Ƃ��Ĉ��]�����Ăł��闧�̂�M�Ƃ���B �@���_��0�Ƃ�����W���ʏ�ɓ_A(��3,0), B(��3,1)������B0��t����3�ɑ���,P(t,0), Q(t�|��3,0), R(t�|��3,1)���Ƃ�B����PR�ƒ���OB�̌�_��C�Ƃ���B5�̐����ň͂܂�镔���̐}�`��,x�������Ƃ��Ĉ��]�����Ăł��闧�̂�M�Ƃ���B(1) �_C�̍��W��t��p���ĕ\���B �y���z C��x���W��(��3�{t�|��3)��2��t/2 ��AOB��30�����,C��y���W��(t/2)�~ �@C(t/2, (2) ����M�̑̐�V��t��p���ĕ\���B �y���z�~������( ��COH�䁢BOA(�䂔:2��3)��,�̐ϔ��t3:24��3
(3) ����M�̕\�ʐ�S��t��p���ĕ\���B �y���zOB��2 S��
|
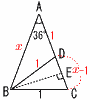 (1) AB��AC,BC��1,��ABC=72���̓ӎO�p�`ABC�ɂ���, (1) AB��AC,BC��1,��ABC=72���̓ӎO�p�`ABC�ɂ���,�@ ���� CD�̒��� �y���z��ABD,��BCD�͓ӎO�p�` AB��AC��x�Ƃ����,��ABC�䁢BCD���, �@x:1��1:(x�|1)��,x2�|x�|1��0
�A BE2�̒l �y���z��BCE��, BE2��BC2�|( 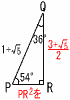 �@�� �@��(2) 1��]���Ăł��闧�̂̑̐� �y���z(1)���,��PQR�䁢ABE(������2:1) QR��2AE��2�~{1�{ PR2��(2BE)2��4BE2��4�~ �̐ρ� �@��
|
||||||||||||||||||||||||||
| �R | �c��`�m���Z�@�i�q�T�N�j�@������ | �U | �s���x�썂�Z�@�i�q�U�N�j�@���� | ||||||||||||||||||||||||
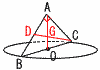 �@��BC���a�Ƃ��锼�a�P�̉~�O�ƕ�BC���ΕӂƂ��钼�p�ӎO�p�`ABC������B �@��BC���a�Ƃ��锼�a�P�̉~�O�ƕ�BC���ΕӂƂ��钼�p�ӎO�p�`ABC������B(1) �ʂ��������̗��̂̑̐ς����߂�B �y���zG�͏d�S��,AG�� (��ABO�̉�]��)�|(��ADG�̉�]��)��, �̐ρ� (2) �ʂ��������̗��̂̕\�ʐς����߂�B �y���z(���aAC�̔���)�|(��ABC�̉�]��)��, �\�ʐρ�(�����̋Ȗʐ�)�{(�~���̑��ʐ�)
|
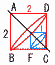 �@�}�̂悤��,1�ӂ̒�����2�ł��鐳���`ABCD������B��AD�̒��_��E,��BC�̒��_��F�Ƃ���B �@�}�̂悤��,1�ӂ̒�����2�ł��鐳���`ABCD������B��AD�̒��_��E,��BC�̒��_��F�Ƃ���B(1) �����`ABCD��,����CD����]�̎��Ƃ���1��]�������Ƃ�,�l�p�`ABFE���ʉ߂��Ăł��闧�̂̑̐ς����߂Ȃ����B �y���z��~���|���~�� �̐ρ�(22�|12)���~2��6�� (2) �����`ABCD��,����AC����]�̎��Ƃ���1��]�������Ƃ�,�l�p�`ABFE���ʉ߂��Ăł��闧�̂̑̐ς����߂Ȃ����B �y���z�ԉ~���F�~����23�F13��8:1 �̐ρ�(��~���~2)�~ �@�� |
||||||||||||||||||||||||||