| 丂俀俈丂夞揮懱 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 丂俀俈丂夞揮懱 | 丂丂丂寧丂丂丂擔乮丂丂乯 |
| 侾 | 惉纥崅峑丂乮俼係擭乯丂仛 | 係 | 嶉嬍導棫崅峑丂乮俼俇擭乯丂仛仛仛 |
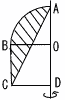 丂恾偺傛偆偵,敿宎3,拞怱妏90亱偺偍偆偓宍OAB偲惓曽宍OBCD傪慻傒崌傢偣偨恾宍偵慄暘AC傪堷偔丅幬慄晹暘傪,捈慄AD傪幉偲偟偰1夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔傛丅 丂恾偺傛偆偵,敿宎3,拞怱妏90亱偺偍偆偓宍OAB偲惓曽宍OBCD傪慻傒崌傢偣偨恾宍偵慄暘AC傪堷偔丅幬慄晹暘傪,捈慄AD傪幉偲偟偰1夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔傛丅丂 |
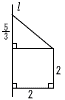 丂塃偺恾偺傛偆側AB亖AC亖2cm,佢BAC亖90亱偺仮ABC偑偁傝,捀揰C傪捠傝,曈BC偵悅捈側捈慄/傪傂偒傑偡丅偙偺偲偒,仮ABC傪,捈慄/傪幉偲偟偰1夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔側偝偄丅 丂塃偺恾偺傛偆側AB亖AC亖2cm,佢BAC亖90亱偺仮ABC偑偁傝,捀揰C傪捠傝,曈BC偵悅捈側捈慄/傪傂偒傑偡丅偙偺偲偒,仮ABC傪,捈慄/傪幉偲偟偰1夞揮偝偣偰偱偒傞棫懱偺懱愊傪媮傔側偝偄丅 |
||
| 俀 | 憗戝杮彲崅摍妛堾丂乮俼俆擭乯丂仛仛仛 | 俆 | 憗戝崅摍妛堾丂乮俼係擭乯丂仛仛仛 |
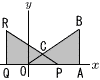 丂尨揰傪0偲偡傞嵗昗暯柺忋偵揰A(併3,0), B(併3,1)偑偁傞丅0亝t亝併3偵懳偟偰,P(t,0), Q(t亅併3,0), R(t亅併3,1)傪偲傞丅捈慄PR偲捈慄OB偺岎揰傪C偲偡傞丅5偮偺慄暘AB,BC,CR,RQ,QA偱埻傑傟傞晹暘偺恾宍傪,x幉傪幉偲偟偰堦夞揮偝偣偰偱偒傞棫懱傪M偲偡傞丅 丂尨揰傪0偲偡傞嵗昗暯柺忋偵揰A(併3,0), B(併3,1)偑偁傞丅0亝t亝併3偵懳偟偰,P(t,0), Q(t亅併3,0), R(t亅併3,1)傪偲傞丅捈慄PR偲捈慄OB偺岎揰傪C偲偡傞丅5偮偺慄暘AB,BC,CR,RQ,QA偱埻傑傟傞晹暘偺恾宍傪,x幉傪幉偲偟偰堦夞揮偝偣偰偱偒傞棫懱傪M偲偡傞丅(1) 揰C偺嵗昗傪t傪梡偄偰昞偣丅 (2) 棫懱M偺懱愊V傪t傪梡偄偰昞偣丅 (3) 棫懱M偺昞柺愊S傪t傪梡偄偰昞偣丅 丂 |
(1) AB亖AC,BC亖1,佢ABC=72亱偺擇摍曈嶰妏宍ABC偵偮偄偰, 嘆 佢ABC偺擇摍暘慄偲曈AC偲偺岎揰傪D偲偡傞偲偒,慄暘 CD偺挿偝傪媮傔傛丅 嘇 捀揰B偐傜曈AC傊悅慄傪傂偒,曈AC偲偺岎揰傪E偲偡傞偲偒,BE2偺抣傪媮傔傛丅 (2) PQ亖1亄併5,佢PRQ= 90亱,佢QPR=54亱偺捈妏嶰妏宍PQR傪曈QR偺傑傢傝偵1夞揮偟偰偱偒傞棫懱偺懱愊傪媮傔傛丅 丂 |
||
| 俁 | 宑滀媊弇崅峑丂乮俼俆擭乯丂仛仛仛 | 俇 | 巗棫杧愳崅峑丂乮俼俇擭乯丂仛仛仛 |
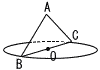 丂曈BC捈宎偲偡傞敿宎侾偺墌侽偲曈BC傪幬曈偲偡傞捈妏擇摍曈嶰妏宍ABC偑偁傞丅墌O傪娷傓暯柺偲仮ABC傪娷傓暯柺偑悅捈偱,曈AB偺拞揰傪揰D偲偡傞偲偒, 丂曈BC捈宎偲偡傞敿宎侾偺墌侽偲曈BC傪幬曈偲偡傞捈妏擇摍曈嶰妏宍ABC偑偁傞丅墌O傪娷傓暯柺偲仮ABC傪娷傓暯柺偑悅捈偱,曈AB偺拞揰傪揰D偲偡傞偲偒,(1) OA傪幉偲偟偰仮BCD傪1夞揮偝偣偨偲偒,仮BCD偲偦偺撪晹偑捠偭偨晹暘偺棫懱偺懱愊傪媮傔傛丅 (2) AB傪幉偲偟偰墌O傪1夞揮偝偣偨偲偒,墌O偲偦偺撪晹偑捠偭偨晹暘偺棫懱偺昞柺愊傪媮傔傛丅 丂丂 |
 丂恾偺傛偆偵,1曈偺挿偝偑2偱偁傞惓曽宍ABCD偑偁傞丅曈AD偺拞揰傪E,曈BC偺拞揰傪F偲偡傞丅 丂恾偺傛偆偵,1曈偺挿偝偑2偱偁傞惓曽宍ABCD偑偁傞丅曈AD偺拞揰傪E,曈BC偺拞揰傪F偲偡傞丅(1) 惓曽宍ABCD傪,捈慄CD傪夞揮偺幉偲偟偰1夞揮偝偣偨偲偒,巐妏宍ABFE偑捠夁偟偰偱偒傞棫懱偺懱愊傪媮傔側偝偄丅 (2) 惓曽宍ABCD傪,捈慄AC傪夞揮偺幉偲偟偰1夞揮偝偣偨偲偒,巐妏宍ABFE偑捠夁偟偰偱偒傞棫懱偺懱愊傪媮傔側偝偄丅 |
||