| 29 四面体 (略解) | ||
| 29 四面体 (略解) | ||
| 1 | 市立西京高校 (R6年) ★★★ | 4 | 巣鴨高校 (R4年) ★★ | ||||||
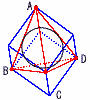 正四面体ABCDに半径1の球が内接している。この正四面体の1辺の長さを求めよ。ただし,内接するとは,球が正四面体のすべての面と接することである。 正四面体ABCDに半径1の球が内接している。この正四面体の1辺の長さを求めよ。ただし,内接するとは,球が正四面体のすべての面と接することである。【解】正四面体=立方体−三角錐×4 1辺aの正四面体= 半径1の球が内接する正四面体= ア=イより, |
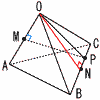 OPの長さと△POMの面積をそれぞれ求めなさい。 OPの長さと△POMの面積をそれぞれ求めなさい。【解】 △ONPで,∠ONP=90°,ON=2√3 OP=√(2√3)2+12=√13 ∠OMP=90°より,△OMPで, MP=√(√13)2−22=3 △POM= |
||||||||
| 2 | 市川高校 (R5年) ★★★ | 5 | 明治大付属明治高校 (R4年) ★★★ | ||||||
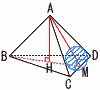 右の図のように,四面体ABCDがあり,AB=AC=AD=√21,CD=2√5,BC=BD=√30である。 右の図のように,四面体ABCDがあり,AB=AC=AD=√21,CD=2√5,BC=BD=√30である。また,CDの中点をM,Aから△BCDに下ろした垂線と△BCDとの交点をHとする。 (1) AMの長さを求めよ。 【解】 △ACMで,AM=√(√25)2−(√5)2=4 (2) AHの長さを求めよ。 【解】 △BCMで,BM=√(√30)2−(√5)2=5 △ABMで,BH=xとすると, AH2=(√21)2−x2=42−(5−x)2で,x=3 AH2=(√21)2−32=12より, AH=√12=2√3 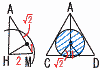 (3) Hを中心として半径√5の球を平面ACDが切りとってできる断面と,△ACDの共通部分の面積を求めよ。 (3) Hを中心として半径√5の球を平面ACDが切りとってできる断面と,△ACDの共通部分の面積を求めよ。【解】斜線部分=扇形+二等辺三角形 面積=(√2)2π× |
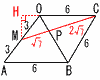 図のように,1辺の長さが6の正四面体OABCがある。辺OAの中点をMとし,辺O上に点PをMP+PCの長さが最短となるようにとる。 図のように,1辺の長さが6の正四面体OABCがある。辺OAの中点をMとし,辺O上に点PをMP+PCの長さが最短となるようにとる。(1) MP+PCの長さ 【解】(右図参照) △MOHで,∠MOH=60°より, OH= △MCHで,MC=√ { ( 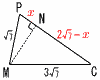 (2) △MPCの面積 【解】△POM∽△PBC(相似比1:2) △MPCで,垂線MNをおろし, PN=xとすると, MN2=(√7)2−x2=(3√7)2−(2√7−x)2 これを解いて,x= △MPC= (3) 小さいほうの立体に内接する球の半径 【解】(右図参照) 三角錐O-MPC=正四面体O-ABC× = △OMC= △OPM= △OPC= 内接球の半径をrとすると,ア〜エより,
|
||||||||
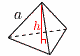 高 さ h= 体 積 V=  表面積S= 表面積S=外接球の半径R= 内接球の半径r= |
|||||||||
| 3 | 日本大第二高校 (R6年) ★★★ | (2) 正四面体ABCDの体積を求めよ。 【解】△NBCは正四面体を,ADと垂直に2等分割している △NBC= 体積= (3) 四面体ABCPの体積を求めよ。 【解】(三角錐A-BNC)+(三角錐P-BNC) AP=xとすると,AP2=MP2=MN2+(AP−AN)2 x2=(3√2)2+(x−3)2より,x=AP= 体積= |
|||||||
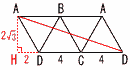 図のように,1辺の長さが6の正四面体ABCDにおいて,2辺BC,ADの中点をそれぞれM,Nとし,辺AD上にAP=MPとなるような点Pをとる。 図のように,1辺の長さが6の正四面体ABCDにおいて,2辺BC,ADの中点をそれぞれM,Nとし,辺AD上にAP=MPとなるような点Pをとる。(1) 線分MNの長さを求めよ。 【解】MNは△NBCの中線 △NBCで,NB=NC=3√3 MN=√(3√32)−32=3√2 (右へつづく→) |
|||||||||