| 30 正八面体 (略解) | ||
| 30 正八面体 (略解) | ||
| 1 | 中央大附属横浜高校 (R4年) ★★ | 4 | 就実高校 (R4年) ★ |
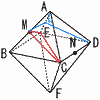 1辺の長さが8の正八面体ABCDEF があり,辺ABの中点をM,辺CDの中点をNとする。 1辺の長さが8の正八面体ABCDEF があり,辺ABの中点をM,辺CDの中点をNとする。(1) 三角すいMBCEの体積を求めなさい。 【解】 体積= = 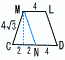 (2) MNの長さを求めなさい。 (2) MNの長さを求めなさい。【解】 等脚台形LMCDで,MC=LD=MN △ABCで,CM=4√3より, MN=CM=4√3 |
 図のような1辺の長さが6cmの立方体がある。この立方体の各面の対角線の交点を結んで正八面体を作るとき,この正八面体の体積は[ ]cm3である。 図のような1辺の長さが6cmの立方体がある。この立方体の各面の対角線の交点を結んで正八面体を作るとき,この正八面体の体積は[ ]cm3である。【解】(右図参照) △OABで, OA=OB=3より, AB=3√2 正八面体の1辺は3√2cmとなって, 体積= |
||
| 2 | 東京学芸大附属高校 (R5年) ★★ | 5 | 慶應義塾志木高校 (R4年) ★★★ |
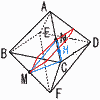 右の図のように,1辺の長さが2cmの正八面体ABCDEFがあり,辺BFの中点をM,辺ACの中点をNとする。 右の図のように,1辺の長さが2cmの正八面体ABCDEFがあり,辺BFの中点をM,辺ACの中点をNとする。(1) △ABFの面積を求めなさい。 【解】正方形ABFDの半分 △ABF=22÷2=2cm2 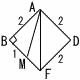 (2) 線分AMの長さを求めなさい。 (2) 線分AMの長さを求めなさい。【解】△ABMは直角三角形 AM=√22+12=√5cm 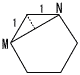 (3) 線分MNの長さを求めなさい。 (3) 線分MNの長さを求めなさい。【解】切り口は正六角形 MN=√3cm (4) △AMNの面積を求めなさい。 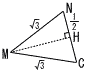 【解】△MNCは二等辺三角形 【解】△MNCは二等辺三角形MH=√(√3)2+(1/2)2= △AMN= |
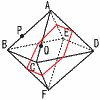 図のような1辺の長さが2の正八面体ABCDEFがあり,辺AB上の点P,辺AC上の点QをAP:PB=AQ:QC=2:1となるようにとる.正八面体ABCDEFを,次のような平面で切るとき,切り口の面積を求めよ。 図のような1辺の長さが2の正八面体ABCDEFがあり,辺AB上の点P,辺AC上の点QをAP:PB=AQ:QC=2:1となるようにとる.正八面体ABCDEFを,次のような平面で切るとき,切り口の面積を求めよ。(1) △DEFに平行で2等分する平面 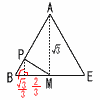 【解】(右上図参照) 【解】(右上図参照)切り口は,1辺1の正六角形 面積=( (2) 線分PQを含み2等分する平面 【解】(右図参照)M,Nは中点 切り口は,六角形で, 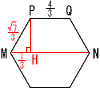 PM=√ { ( PM=√ { (PH=√ { ( 面積=台形PMNQ×2 = |
||
| 3 | 明治学院東村山高校 (R6年) ★★ | 6 | 鎌倉学園高校 (R6年) ★★ |
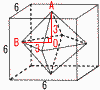
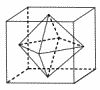 図1のように,立方体に正八面体が接しています。また,図2はI,L,J,Nを通る平面で切断した断面です。 図1のように,立方体に正八面体が接しています。また,図2はI,L,J,Nを通る平面で切断した断面です。(1) 立方体の1辺の長さが8cmのとき,正方形I LJNの1辺の長さを求めなさい。 【解】4√2cm (2) 四角形KLMNの面積が32cm2のとき,立方体の1辺の長さを求めなさい。 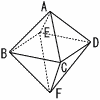 【解】KL=LJ=4√2より, 8cm 【解】KL=LJ=4√2より, 8cm(3) (2)のとき,正八面体の体積を求めなさい。 【解】(正四角錐I-KLMN)×2 正四角錐I-KLMNの高さIO= 体積=( |
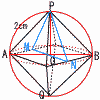 1辺が2cmである正八面体があります。 1辺が2cmである正八面体があります。(1) この正八面体に外接する球の半径を求めなさい。 【解】△OAPの等辺 半径=OA= 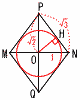 (2) この正八面体に内接する球の半径を求めなさい。 (2) この正八面体に内接する球の半径を求めなさい。【解】切断面PMQNで考える △ONH∽△PNO(3辺は1:√2:√3) 半径=OH=PO÷√3=√2÷√3= |
||
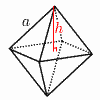 高 さ h= 体 積 V= 表面積S=2√3a2 |
|||