| 31 多面体 (略解) | ||
| 31 多面体 (略解) | ||
| 1 | 西大和学園高校 (R4年) ★★ | 4 | 慶應義塾志木高校 (R6年) ★★★ | |||||
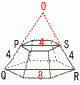 このとき,図2の立体の体積を求めよ。 このとき,図2の立体の体積を求めよ。【解】切断面PQRSを考える PQ,SRの延長交点Oをとると, 正六角錐O-PS∽正六角錐OーQR (相似比は1:2)…ア 正六角錐OーQR= 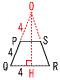 = =アイより, 体積=正六角錐OーQR× =96× |
多面体の各頂点に集まる各辺を3等分する点のうち,頂点に近い方の点をすべて通る平面で立体を切り,頂点を含む角錐を取り除いて新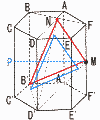 しい立体を作る操作を[操作1]とする。例えば図1の正四面体に[操作1]をすると,図2のような立体ができる。 しい立体を作る操作を[操作1]とする。例えば図1の正四面体に[操作1]をすると,図2のような立体ができる。(1) 図3のような1辺の長さが9の正八面体に[操作1]をしたときにできる立体の体積V1を求めよ。 【解】 正四角錐P-ABCD= 切り取る小四角錐=ア× 体積V1=ア×2-イ×6=243√2-27√2=216√2 (2) (1)でできた立体に対して,さらに[操作1]をしたときにできる立体の体積V2を求めよ。 【解】図2(切頂八面体)は,正方形6,正六角形8,頂点14 切り取る小三角錐= 体積V2=V1- |
|||||||
| 2 | 筑波大附属駒場高校 (R5年) ★★★ | |||||||
 (1) 面が一辺10cmの正方形で,側面が一辺10cmの正三角形である正四角すいの体積 (1) 面が一辺10cmの正方形で,側面が一辺10cmの正三角形である正四角すいの体積【解】 体積= (2) 一辺10cmの正方形6個と一辺10cmの正六角形8個で作られた多面体(切頂八面体という)の体積 【解】一辺30cmの正八面体-(1)×6
|
||||||||
| 3 | 洛南高校 (R5年) ★★★ | 5 | 早稲田大高等学院 (R5年) ★★★ | |||||
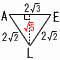 (1) すべての辺の長さが2の正六角柱ABCDEF-GHIJKLがあります。 (1) すべての辺の長さが2の正六角柱ABCDEF-GHIJKLがあります。(ア) △AELの面積(右図) 【解】二等辺三角形 △AEL= (イ) 四面体AEILの体積 【解】(三角錐A-MLI)-(三角錐E-MLI) 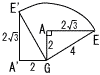 体積=2( 体積=2((2) (ア) 手順①で通過する面積 【解】△AGE+扇形GEE'(右上図) 面積= 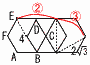 (イ) 手順①~④で曲線の長さの和 【解】 手順②=8π× 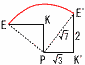 Eが描く曲線PE=√22+(√3)2=√7 Eが描く曲線PE=√22+(√3)2=√7手順④=2√7π× 長さの和=(2+
|
図1,図2のような多面体Pについて考える。 (1) 多面体P(正四角反柱という)の表面積 【解】正方形2個+正三角形8個 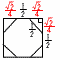 表面積=12×2+ 表面積=12×2+(2) 断面の図形の面積 【解】1辺 断面積=( (3) 周の長さを求めよ。 【解】四角形DGEA 周の長さ=√2+1×3=√2+3 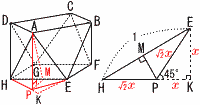 (4) h2の値を求めよ。 【解】h=APとする △EHKで, (√2x+x)2+x2=12 x2=1/(4+2√2) △APMで,h2=AM2-PM2=AM2-(PE2-EM2) =( |
|||||||