| 32 球 (略解) | ||
| 32 球 (略解) | ||
| 1 | 都立産業技術高専 (R5年) ★★ | 4 | 久留米大附設高校 (R6年) ★★ |
| 半径rcmの球が,点Pで平面Hと接している。 (1) r=3のとき,球Oの体積 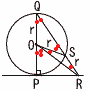 【解】球O= 【解】球O=(2) ∠SQOと∠ROPの比 【解】△SORと△OSQは二等辺三角形 ∠SQO=2aとすると,∠ROP=3aで, 2:3 (3) 線分QSの長さ 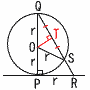 【解】OからQRに垂線OTをおろす 【解】OからQRに垂線OTをおろす△PQRで,QR=√(2r)2+r2=√5r △QTO∽△QPR(比1:√5)より, QT=2r×(1/√5)= QS=2QT= |
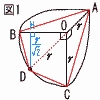 (1) 1辺の長さが10の正四面体の高さを求めよ。 (1) 1辺の長さが10の正四面体の高さを求めよ。【解】△OAMで考える h2=102-x2=(5√3)2-(5√3-x)2 これを解いて,x= 高さh=√ {100-( 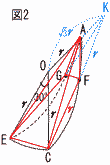 (2) 右図のように正三角柱の中に下の段から順に6個,3個,1個の半径1の球が互いに接するように積んである。最下段の6個の球はすべて正三角柱の底面と側面にも接している。また,最上段の球は正三角柱の上面に接している。この正三角柱の高さを求めよ。 (2) 右図のように正三角柱の中に下の段から順に6個,3個,1個の半径1の球が互いに接するように積んである。最下段の6個の球はすべて正三角柱の底面と側面にも接している。また,最上段の球は正三角柱の上面に接している。この正三角柱の高さを求めよ。【解】 高さ=(1辺4の正四面体の高さ)+(球の半径)×2 = |
||
| 2 | 中央大附属高校 (R4年) ★★ | 5 | 明大付属中野八王子高校 (R4年) ★★ |
| 粘土でできた表面積が16πである球を体積の等しい8つの小球に分割するとき,8つの小球の表面積の和を求めなさい。 【解】大球∽小球(相似比2:1) 体積比=8:1より,表面積比=4:1で, 小球の表面積の和=16π× |
縦,横,高さが4cm,5cm,7cmの直方体のすべての頂点を通る球の表面積を求めなさい。 【解】直方体の対角線=外接球の直径 球の半径をrとすると, 2r=√42+52+72=3√10で,r= 表面積=4π×( |
||
| 3 | 大阪産大附属高校 (R4年) ★★★ | 6 | 桐蔭学園高校 (R6年) ★★ |
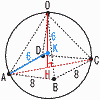 図のように,5点O,A,B,C,Dは球の表面上 の点であり,立体O-ABCDは正四角錐である。球の半径が6cm,AB=8cmのとき, 図のように,5点O,A,B,C,Dは球の表面上 の点であり,立体O-ABCDは正四角錐である。球の半径が6cm,AB=8cmのとき,(1) 球の体積を求めなさい。 【解】 体積= 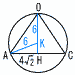 (2) ACの長さを求めなさい。 【解】 △ABCで,AC=√82+82=8√2cm (3) 正四角錐O-ABCDの体積を求めなさい。 【解】球の中心をKとすると, △KAHで,KH=√62-(4√2)2=2で, OH=6+2=8 体積= (4) 正四角錐O-ABCDの表面積を求めなさい。 【解】 △OAHで,OA=√(4√2)2+82=4√6 ABの中点をMとすると,△OAMで, OM=√(4√6)2-42=4√5 表面積=( |
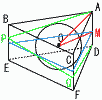 右の図のように,1辺の長さが4である正三角形を底面とする正三角柱ABC-DEFがある。この正三角柱のすぺての面に接する球Oがある。 右の図のように,1辺の長さが4である正三角形を底面とする正三角柱ABC-DEFがある。この正三角柱のすぺての面に接する球Oがある。(1) 球の半径は[ ]であり,正三角柱の体積は[ ]である。 【解】水平に2等分割するとき, 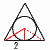 円Oは正三角形(1辺4)の内接円 円Oは正三角形(1辺4)の内接円半径=2÷√3= 体積=( (2) 球の中心をOとするとき,0A=[ ]である。 【解】OM=中線× OA=√ { ( 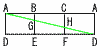 (3) 辺BE上に点G,辺CF上に点Hをとり,AG+GH+HDが最小になるときを考える。このとき,BG=[ ]である。 (3) 辺BE上に点G,辺CF上に点Hをとり,AG+GH+HDが最小になるときを考える。このとき,BG=[ ]である。【解】側面の展開図で考える BG= (4) (3)でとった点G,Hと点Aを通る平面でこの立体を切る。点Dを合むほうの立体の体積は[ ]である。 【解】立体は切頭三角柱(斜めにカット) 体積=(底面積)×(高さの平均) =4√3× |
||