 図形 |
３２ 球 | 月 日（ ） |
| 図形 |
３２ 球 | 月 日（ ） |
| １ | 都立産業技術高専 （Ｒ５年） ★★ | ４ | 久留米大附設高校 （Ｒ６年） ★★ |
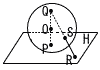 図は,点Oを中心とする半径rcmの球が,点Pで平面Hと接する場合を表している。 ただし,r＞0とする。半直線POと球の表面との交点をQとし,点Pと点Qを結ぶ。点Rは平面H上にある点で,点Pと一致しない。点Qと点Rを結び,線分QRと球の表面との交点をSとする。(1) r＝3のとき,球Oの体積は何cm3か。 (2) 点Oと点Rを結ぶ。線分SRの長さがrcmのとき,∠SQOの大きさと∠ROPの大きさの比を最も簡単な整数の比で表せ。 (3) 点Pと点Rを結ぶ。線分PRの長さがrcmのとき,線分QSの長さは何cmか。rを用いた式で表せ。 |
(1) １辺の長さが10の正四面体の高さを求めよ。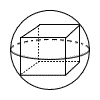 (2) 右図のように正三角柱の中に下の段から順に6個,3個,1個の半径1の球が互いに接するように積んである。最下段の6個の球はすべて正三角柱の底面と側面にも接している。また,最上段の球は正三角柱の上面に接している。この正三角柱の高さを求めよ。 |
||
| ２ | 中央大附属高校 （Ｒ４年） ★★ | ５ | 明大付属中野八王子高校 （Ｒ４年） ★★ |
| 粘土でできた表面積が16πである球を体積の等しい8つの小球に分割するとき,8つの小球の表面積の和を求めなさい。 |
縦,横,高さが4cm,5cm,7cmの直方体のすべての頂点を通る球の表面積を求めなさい。 |
||
| ３ | 大阪産大附属高校 （Ｒ４年） ★★★ | ６ | 桐蔭学園高校 （Ｒ６年） ★★ |
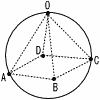 図のように,5点O,A,B,C,Dは球の表面上 の点であり,立体O-ABCDは正四角錐である。球の半径が6cm,AB＝8cmのとき,次の問いに答えなさい。ただし,円周率をπとし,球の中心は正四角錐の内側にあるものとする。(1) 球の体積を求めなさい。 (2) ACの長さを求めなさい。 (3) 正四角錐O-ABCDの体積を求めなさい。 (4) 正四角錐O-ABCDの表面積を求めなさい。 |
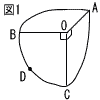 右の図のように,1辺の長さが4である正三角形を底面とする正三角柱ABC-DEFがある。この正三角柱のすぺての面に接する球Oがある。(1) 球の半径は[ ]であり,正三角柱の体積は[ ]である。 (2) 球の中心をOとするとき,０Ａ＝[ ]である。 (3) 辺ＢＥ上に点G,辺CF上に点Hをとり,ＡG＋GH＋HDが最小になるときを考える。このとき,BG＝[ ]である。 (4) (3)でとった点G,Hと点Aを通る平面でこの立体を切る。点Dを合むほうの立体の体積は[ ]である。 |
||
