| 1 |
和歌山県立高校 (R5年) ★ |
5 |
専修大附属高校 (R4年) ★ |
| 通学時間(分) |
度数(人) |
相対度数 |
累積度数(人) |
以上 未満
0〜10 |
24 |
* |
* |
| 10〜20 |
56 |
* |
* |
| 20〜30 |
64 |
0.32 |
イ |
| 30〜40 |
40 |
0.20 |
* |
| 40〜50 |
16 |
ア |
* |
| 計 |
200 |
1.00 |
- |
次の表は,ある学年の生徒の通学時間を調査し,その結果を度数分布表にまとめたものである。表中のア,イにあてはまる数をそれぞれ求めなさい。
【解】
ア 16÷200=0.08 イ 24+56+64=144 |
| 点数(点) |
度数(人) |
以上 未満
30〜40 |
3 |
| 40〜50 |
x |
| 50〜60 |
16 |
| 60〜70 |
y |
| 70〜80 |
2 |
| 合 計 |
40 |
右の表はあるクラス40人の数学のテストの点数を度数分布表に整理したものである。 50点未満の生徒の人数が全体の30%であったとき,x,yの値を求めなさい。
【解】
50点未満=3+x=40×0.3
x=12−3=9
50点以上=16+y+2=40×0.7
y=28−16−2=10 |
| 2 |
鹿児島県立高校 (R4年) ★ |
6 |
福岡県立高校 (R4年) ★ |
| − |
選手数 |
女性の割合 |
| 1964年 |
5151人 |
約13% |
| 2021年 |
11092人 |
約49% |
表は,1964年と2021年に開催された東京オリンピックに参加した選手数と,そのうちの女性の選手数の割合をそれぞれ示したものである。2021年の女性の選手数は,1964年の女性の選手数の約何倍か。最も適当なものを下のア〜工の中から1つ選び,記号で答えよ。
ア 約2倍 イ 約4倍 ウ 約8倍 工 約12倍
【解】
| 2021年 |
= |
11092×0.49 |
≒ |
2×4 |
≒8 |
ウ |
| 1964年 |
5151×0.13 |
1×1 |
|
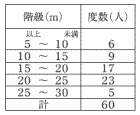 右の表は,M中学校の1年生男子のハンドボール投げの記録を度数分布表に整理したものである。 右の表は,M中学校の1年生男子のハンドボール投げの記録を度数分布表に整理したものである。
この表をもとに,記録が20m未満の累積相対度数を四捨五入して小数第2位まで求めよ。
【解】
| 20m未満の |
= |
6+9+17 |
= |
32 |
=0.5333…≒0.53 |
| 累積相対度数 |
60 |
60 |
|
| 3 |
高知県立高校 (R4年) ★ |
7 |
滋賀県立高校 (R4年) ★ |
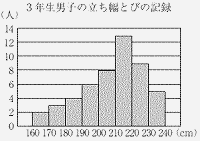 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。
このヒストグラムにおいて,3年生男子50人をもとにした,立ち幅とびの記録が200cm以上230cm未満の生徒の人数の割合は何%か。
| 【解】200〜230cm= |
8+13+9 |
×100= |
30 |
×100=60% |
| 50 |
50 |
|
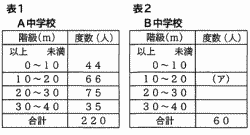 表1は,A中学校におけるハンドボール投げの記録を度数分布表に整理したものです。表1をもとに,表2のB中学校の度数分布を推定します。A中学校とB中学校の10m以上20m未満の階級の相対度数が等しいとしたとき,表2の(ア)にあてはまる度数を求めなさい。 表1は,A中学校におけるハンドボール投げの記録を度数分布表に整理したものです。表1をもとに,表2のB中学校の度数分布を推定します。A中学校とB中学校の10m以上20m未満の階級の相対度数が等しいとしたとき,表2の(ア)にあてはまる度数を求めなさい。
【解】
ア=66×60÷220=18 |
| 4 |
大阪産大高校 (R6年) ★ |
8 |
神戸学院大附属高校 (R6年) ★ |
| 点数(点) |
度数(人) |
| 男子 |
女子 |
| 0以上10未満 |
x |
4 |
| 10 〜 20 |
y |
x |
| 20 〜 30 |
6 |
y |
| 30 〜 40 |
11 |
9 |
| 40 〜 50 |
8 |
7 |
| 計 |
40 |
35 |
右の表は,男子40人と女子35人の50点満点の数学のテストの結果を,度数分布表に整理したものである。 このテストでは満点である50点の生徒はおらず,男女別に各階級の相対度数を求めたところ,10点以上20点未満の階級の相対度数が等しくなりました。x,yの値をそれぞれ求めなさい。
| 【解】 |
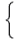 |
x+y=15…ア |
|
y |
= |
x |
…イ |
|
40 |
35 |
アイを連立させて解くと, x=7, y=8 |
| 階級 |
度数 |
相対 |
| 50〜 |
4 |
ア |
| 60〜 |
3 |
|
| 70〜 |
6 |
|
| 80〜 |
2 |
イ |
| 90〜 |
1 |
|
| 計 |
16 |
|
下の数は,あるクラスの生徒16名の数学のテストの得点である。度数分布表のア,イに入る数を,小数第3位を四捨五入して小数第2位まで求めなさい。
56 70 89 67 66 73 62 75 74
53 77 58 74 80 92 56 |
【解】各階級の度数を数える
ア=4÷16=0.25
イ=2÷16≒0.13
|
 右の表は,M中学校の1年生男子のハンドボール投げの記録を度数分布表に整理したものである。
右の表は,M中学校の1年生男子のハンドボール投げの記録を度数分布表に整理したものである。 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。
右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。 表1は,A中学校におけるハンドボール投げの記録を度数分布表に整理したものです。表1をもとに,表2のB中学校の度数分布を推定します。A中学校とB中学校の10m以上20m未満の階級の相対度数が等しいとしたとき,表2の(ア)にあてはまる度数を求めなさい。
表1は,A中学校におけるハンドボール投げの記録を度数分布表に整理したものです。表1をもとに,表2のB中学校の度数分布を推定します。A中学校とB中学校の10m以上20m未満の階級の相対度数が等しいとしたとき,表2の(ア)にあてはまる度数を求めなさい。