データの活用

３　代表値２　（略解）

１	近畿大附属和歌山高校　（Ｒ５年）　★	５	函館・ラサール高校　（Ｒ４年）　★
次の資料は,8人の生徒が1年間で読んだ本の冊数である。 　 12，5，3，9，13，6，2，a　(単位は冊) 　8人の冊数の中央値が7であるときaの値を求めよ。ただし,aは0以上の整数である。 【解】 昇順に並び替えて 　2, 3, 5 6, a, 9, 12, 13 中央値＝(6＋a)÷2＝7より, a＝8		次の表は2020年のH市の毎日の最低気温の月別平均を示したものです。12個のデータ の範囲と中央値を求めなさい。 1月 2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 -0.9 -0.7 4.1 6.7 12.8 17.8 20.7 23.4 20.0 12.8 7.0 -1.3 【解】 範囲＝最大値−最小値＝23.4−(−1.3)＝24.7 データを順に並べ替えると, 　−1.3,−0.9,−0.7,4.1,6.7, 7.0 , 12.8 ,12.8, 　17.8,20.0,20.7,23.4 中央値＝(7.0＋12.8)÷2＝19.8÷2＝9.9
２	作陽高校　（Ｒ５年）　★	６	就実高校　（Ｒ４年）　★
階級 (点) 度数(人) 0以上5未満 2 5 〜 10 6 10 〜 15 8 15 〜 20 4 計 20 　右の表は,あるクラスの20点満点のテストをした結果をまとめた度数分布表である。中央値は(　　)点であり,平均値は(　　)である。 【解】 10,11番目は10〜15点 　中央値＝(10＋15)÷2＝12.5 (階級値×度数)の合計より, 　平均値＝(2.5×2＋…＋17.5×4)÷20 　　　　＝220÷20＝11		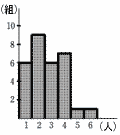x,y,zの関係を正しく表している不等式を解答群から選ぶ 　[解答群] 　ア x＜y＜z　　イ x＜z＜y 　ウ y＜x＜z　　エ y＜z＜x 　オ z＜x＜y　　カ z＜y＜x　 【解】 平均値x＝(6＋18＋18＋28＋5＋6)÷30＝2.7 中央値y＝(2＋3)÷2＝2.5　最頻値z＝2 　z＜y＜xで, カ
３	立命館慶祥高校　（Ｒ４年）　★	７	都立青山高校　（Ｒ４年）　★★
回数(回) 0 1 2 3 4 5 6 7 8 計 度数(人) 0 2 3 2 1 12 10 4 40 　右の表は,中学生40人がバスケットボールのフリースローを 1人8回ずつ行い,シュートが入った回数をまとめたもので,シュートが入った回数が5回の生徒の人数はわかっていない。このとき,40人のシュートが入った回数の平均値を求めなさい。 【解】 5回＝40−(2+3+2+1+12+10+4)＝6人 平均値＝(2+6+6+4+30+72+70+32)÷40 　　＝222÷40＝5.55回		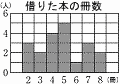4月に図書館で借りた本の冊数を調べたところ,次のような結果になった。 　4，5，2，a，7，6，5，4，b， 　2，c，8，5，3，4，d，4，3，7，5 このとき,整数a,b,c,d の平均値はいくつか。 【解】 グラフより, 　合計冊数＝6+6+16+25+6+21+16＝96冊 数値データより,74＋a＋b＋c＋d＝96 　4数の平均値＝(96−74)÷4＝22÷4＝5.5
４	明治学院高校　（Ｒ６年）　★	８	府立嵯峨野高校　（Ｒ６年）　★★★
A B C D E F G H I J 点数 x y 4 5 6 8 8 9 8 6 　右の表は,10人にテストを行った結果である。テストは10問で１問１点,中央値が6.5点,平均値が6.4点てあるとき,x,yの値を求めよ。ただし,x≦yとする。 　 【解】 順に並べると,〇,4,5,6,6,7,8,8,8,9 中央値が6.5点だから, y＝7 平均値より,x＋y＝10(x≦y)より, x＝3		9人の生徒にテストを行ったところ,得点は次のようになった。ただし,得点はすべて整数である。　 16, 8, x, 13, 11, 12, 8, 15, 7 　このとき,平均値と中央値が同じであった。xのとる値をすぺて求めよ。 【解】平均値＝(90＋x)÷9＝中央値となるxを探す ・xが中央値なら,7,8,8,11,x,12,13,15,16で,x＝11か12（不適） ・xが下位なら,7,8,8,11,12,13,15,16で,x＝0〜11(x＝9で適) ・xが上位なら,7,8,8,11,12,13,15,16で,x＝13〜(x＝18で適) 　よって, x＝9,18

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難