データの活用 ４　代表値３　（略解）
１ 須磨学園高校　（Ｒ４年）　★★ ６ 都立 西 高校　（Ｒ５年）　★
　x,yの値の組み合わせをすべて求めな さい。
【解】中央値は8人目
x＋y＝15−10＝5…ア
得点(点) 0 1 2 3 4 5 合計
生徒数(人) 1 x 3 2 y 4 15
1＋x＋3＋2≦7より,
　x≦1…イ
y＋4≧8より,y≧4…ウ
アイウより, (x,y)＝(0,5) (1,4)
得点(点) 0 5 10 15 20 計
度数(人 2 x 3 y 11 40
　中央値が12.5点であるとき, x,y の値を求めよ。
【解】
下位(0,5,10)と上位(15,20)に等分できる
2＋x＋3＝20, y＋11＝20より
　x＝15　y＝9
　
２ 鎌倉学園高校　（Ｒ４年）　★★ ７ 大阪教育大平野校舎　（Ｒ５年）　★
得点(点) 0 1 2 3 4 5 計
人数(人) 2 4 x 9 y 8 45
(1) xとyの値を求めなさい。
【解】
x＋y＝45−23＝22 …ア
0＋4＋2x＋27＋4y＋40＝3.4×45
　2x＋4y＝153−71＝82 …イ
アイより, x＝3,y=19
(2) 得点が4点の生徒は何人以上何人以下か。
【解】中央値は23人目
2＋4＋x≦22より,x≦16
　アより,x＝22−y≦16で,y≧6 …ウ
y＋8≦22より,y≦14 …エ
ウエより, 6人以上14人以下		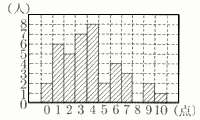 　図は,40人で的あてゲームを行つた得点と人数を表したヒストグラムである。
　このデータについて,以下のものを求めなさい。
(1) 得点の最頻値
【解】
最多は8人で,4点

(2) 40人の得点の平均値
【解】
(1×6＋2×5＋…＋9×2＋10)÷40
　　＝152÷40＝3.8点

(3) 得点の中央値
【解】
20番目は3点で,21番目は4点
(3＋4)÷2＝3.5点
３ 初芝橋本高校　（Ｒ４年）　★★
生徒 A B C D E
基準との差(点) -5 +8 +2 -8 +13
　5人の得点の平均を求めなさい。
【解】
平均値＝ −5＋8＋2−8＋13 ＋80＝2＋80＝82点
5
４ 愛知県立高校A　（Ｒ４年）　★★ ８ 慶應義塾高校　（Ｒ４年）　★★
　aの値を求めなさい。
　1, 3, 5, a, 10, 12　(単位：冊)


【解】
平均値＝ 1＋3＋5＋a＋10＋12 ＝ a＋31 …ア
6 6
中央値＝ 5＋a …イ
2
ア＝イより,a＋31＝3(5＋a)で, a＝8		 　X＝[　　],Y＝[　　]である。
【解】
総得点＝26＋X＋42＋50＋Y＋75＋93＝54×7
　X＋Y＝378−286＝92 …ア
平均点差＝ Y＋218 − X＋68 ＝35
4 3
　3(Y＋218)−4(X＋68)＝35×12
　−4X＋3Y＝38 …イ
アイより, X＝34,Y＝58
５ 都立国立高校　（Ｒ６年）　★★ ９ 都立青山高校　（Ｒ６年）　★
　a,bを1以上6以下の自然数とする。
　4個の数a,b,2,6において,中央値と平均値が一致するa,bの組合せは全部で何通りあるか。
【解】以下の7通り
4数 平・中 a,b
1,2,5,6 3.5 ×2
2,2,6,6 4 ×2
2,3,5,6 4 ×2
2,4,4,6 4 ×1
　次の表は,20人の生徒に5点満点のテストを行ったとき,3点を基準にして,得点から基準を引いた値ごとの人数をまとめたものである。
　このテストの平均点が3.4点のとき,表中のmの値を求めよ。
得点から基準を引いた値(点) -3 -2 -1 0 1 2
人　数　（人） 0 1 m 5 n 4
【解】人数より,m＋n＝10…ア
平均点より,0−2−m＋0＋n＋8＝(3.4−3)×20
　整理すると,−m＋n＝2…イ
(ア−イ)÷2より, m＝4

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難