データの活用 ５　四分位数・箱ひげ図１　（略解）
１ 徳島県立高校　（Ｒ４年）　★ ４ 国立高専　（Ｒ４年）　★
13, 7, 19, 10, 5, 11,
14, 20, 7, 8, 16 (点)
　表は,クイズ大会に参加した11人の得点である。a,bの値をそれぞれ求めなさい。
【解】順に並べ替えると,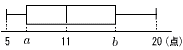
　5,7, 7 ,8,10, 11 ,13,14, 16 ,19,20
中央値が,6番目の11だから,
　第1四分位数(3番目)で, a＝Q1＝7
　第3四分位数(9番目)で, b＝Q3＝16		 　ある試験における10名の生徒の点数は,下の表のようになった。このとき,点数のデータの第2四分位数(中央値)は[　　]点である。また,第3四分位数は[　　]点である。
生　徒 A B C D E F G H I J
点数(点) 2 4 2 7 2 2 7 10 2 4
【解】得点を小さい方から順に並べ替えると,
　2,2,2,2, 2, 4,4 7 ,7,10
中央値は,5・6番目だから, Q2＝(2＋4)÷2＝3点
第3四分位数は8番目だから, Q3＝7点
２ 鹿屋中央高校　（Ｒ４年）　★★ ５ 筑波大附属高校　（Ｒ４年）　★★
階　級
　（分）		 度数
(人)		 累積
度数
以上 未満
0 ～ 5
5
5
5～10 x
10～15 10
15～20 12
20～25 y
25～30 6 50
計 50 －
　ある中学校で,3年生50人の生徒の通学時間について調べた。下の表は,生徒50人の通学時間を度数分布表に整理したものであり,図は.箱ひげ図に整理したものである。
(1) 20分以上25分未満の累積度数
【解】
25分以上が6人だから,
　50－6＝44人
(2) ,第1四分位数がふくまれる階級の階級値を答えよ。
【解】
箱ひげ図より11分で,10～15分の階級
　(10＋15)÷2＝12.5分
(3) 第3四分位数は何番目の生徒の通学時聞か,答えよ。
【解】
四分位数は,Q1が13番目,Q2が25.5番目
　第3が 38番目
(4) x,yの組のうち,yの値がもっとも小さくなる組を求めよ。
【解】
箱ひげ図より,Q1(13番目)は10～15分
xの最大は,0～10分が12人のときだから,
　5＋x＝12で, x＝7　y＝10		 　テストを8人が受けたとき,結果を右のような箱ひげ図になった。このとき,平均点は[　　]点である。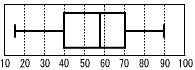
【解】箱ひげ図より,
8人の四分位数は,
Q1が2.5番目で40点で,
　2番目＋3番目＝80点
Q2が4.5番目で57.5点で,
　4番目＋5番目＝115点
Q3が6.5番目で70点で, 6番目＋7番目＝140点
さらに,1番目は15点,8番目は90点
　平均点＝(15＋80＋115＋140＋90)÷8＝55点
６ 早稲田実業高等部　（Ｒ４年）　★★
得点(点) 2 3 4 5 6 7 8 9
人数(人) 3 8 6 10 7 4 1 1
　右の表は,あるクラスの小テストの結果をまとめたものである。この得点データを箱ひげ図に表せ。
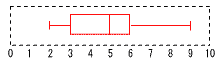
【解】40人の箱ひげ図では,最小値＝2点, 最大値＝9点
　Q1(10.5番目)＝3点, Q2(20.5番目)＝5点
　Q3(30.5番目)＝6点,
　
３ 滝川第二高校　（Ｒ６年）　★★ 【解】
①
　		 ＡグループとBグループの範囲および四分位範囲はそれぞれ等しい。〇　ともに4点
② Bグループは７点以上の人が5人いる。△　6人のときもある
③ Aグループの最高点は１人である。△　2人のときもある
④
　		 Bグループの最高点は１人である。〇
　　　　　　　Q3＝8だから2人にならない
(2) Aグループの平均点を求めなさい。
【解】5点
A＝{ 1 a b c d e f 9 }で,a＋b＝6,c＋d＝10,e＋f＝14
平均点＝(1＋ａ＋ｂ＋…＋9)÷8＝(30＋1＋9)÷8＝5
(3) Bグループの平均点は何点以上であるか答えなさい。
【解】6点以上
B＝{ 2 a b c d e f g 10 }で,a＋b＝8,c≧4,ｄ≧7,,e＋f＝16
平均点≧(2＋ａ＋ｂ＋…＋10)÷9＝(35＋2＋7＋10)÷9＝6
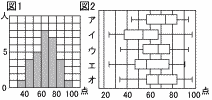　下の図2のア～オの箱ひげ図から,図1に対応するものを選び,記号で答えなさい。
【解】ウ
最小値＝35,最大値＝95,Q1＝55,,Q3＝75
４ お茶の水女子大附属高校　（Ｒ６年）　★★★
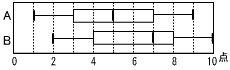　箱ひげ図は,小テストの結果を表している。
(1) 次の①～④について,正しいものには〇,間違っているものには×,正誤が判断できないものには△を記入しなさい。
　　　　　　　　　　(右へつづく→)

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難