データの活用

６ 四分位数・箱ひげ図２　（略解）

１	福井県立高校　（Ｒ５年）　★	５	日大明誠高校　（Ｒ４年）　★
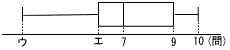ア〜エと,四分位範囲 (データ)　　3, 4, 6, 6, ア, 8, 8, 9, 9, イ 【解】 中央値＝(ア＋8)÷2＝7より, ア＝6 最大値＝イ＝10　最小値＝ウ＝3 第1四分位数(3番目)＝エ＝6		このデータの四分位範囲は[　　]である。 点数(点) 0 1 2 3 4 5 6 7 8 9 10 人数(人) 0 2 1 1 2 8 10 2 4 8 2 【解】 Q1(10,11番目ともに)＝5点 Q3(30,31番目の中間)＝(8＋9)÷2＝8.5点 　四分位範囲＝Q3−Q1＝8.5−5＝3.5点
２	岡山県立高校　（Ｒ４年）　★	６	兵庫県立高校　（Ｒ４年）　★
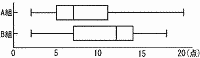正しく説明しているのは,ア〜工のうちではどれですか。 ア 四分位範囲は,A組よりもB組の方が大きい。 イ 2クラス全体の中で,得点が一番高い生徒はB組にいる。 ウ A組の第3四分位数は,B組の第2四分位数より大きい。 エ 得点が12点以上の生徒の人数は,B組がA組の2倍以上である。 【解】アエ ア Aは11−5＝6点,Bは14−7＝7点(正) イ 最大値はAの20点(誤) ウ AのQ3＝11点,BのQ2＝12点(誤) エ Aは10人未満,Bは20人(正）		この図から読み取れることとして正しいものを,あとのア〜エから全て選んで,その符号を書きなさい。 ア 数学,英語どちらの教科も平均点は60点である。 イ 四分位範囲は,英語より数学の方が大きい。 ウ 数学と英語の合計得点が170点である生徒が必ずいる。 エ 数学の得点が80点である生徒が必ずいる。 【解】イエ ア 等しい60点は中央値(誤) イ 数は80−50＝30点,英は70−45＝25点(正) ウ 最大値は不明(誤) エ 数のQ3(27番目)＝80点(正)
３	新潟県立高校　（Ｒ４年）　★★	７	奈良大附属高校　（Ｒ４年）　★
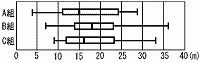正しいものを,ア〜オからすべて選び,その符号を書きなさい。 ア A組,B組,C組のいずれの組にも,30mを上回った生徒がいる。 イ A組とB組を比べると,四分位範囲はB組の方が大きい。 ウ B組とC組を比べると,範囲はB組の方が大きい。 エ 　 A組は,10m以上15m以下の生徒の人数より,15m以上20m以下の生徒の人数の方が多い。　 オ C組には,25m以下だった生徒が27人以上いる。 【解】ウオ ア Aの最大値＝28点(誤) イ Aは24−11＝13点,Bは22.5−14＝8.5点(誤) ウ Bは36−7＝29点,Cは33−12＝11点(正) エ 11〜15mが9人,15〜24mが9人(誤) オ Q3より,23m以下が27人(正)		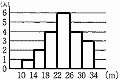右の図は,ある中学校の生徒20人のハンドボール投げの記録をヒストグラムに表したものである。 (1) 26m以上は全体の何％か 【解】 (4＋3)÷20×100＝35％ (2) 平均値を求めなさい。 【解】23.8m (12＋32＋80＋144＋112＋96)÷20＝476÷20＝23.8m (3) 正しいものをア〜エから1つ選び答えなさい。 【解】ウ Q1＝20　Q2＝24　Q3＝28
４	就実高校　（Ｒ６年）　★	８	長野県立高校　（Ｒ６年）　★
箱ひげ図として正しいものを,下のア〜エから選ぶと[　　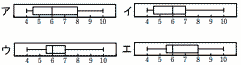] 生　徒 A B C D E F G H I J K L 得点(点) 4 9 6 7 6 7 4 6 4 7 10 5 【解】イ 順に並べると,4 4 4 5 6 6 6 7 7 7 9 10 Q1＝4.5,Q2＝6,Q3＝7		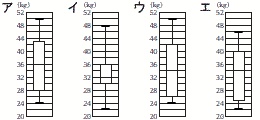24、26、26、26、28、30、32、34、 36、38、40、42、44、48、50 　箱ひげ図として正しいもの 【解】ウ Q1＝26 Q2＝34 Q3＝42

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難