 データの活用 |
１０ 場合の数３ （略解） |
| データの活用 |
１０ 場合の数３ （略解） |
| １ | 桜美林高校 （Ｒ５年） ★★★ | ４ | 白陵高校 （Ｒ４年） ★★ | |||||||||||
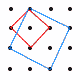 図のように,縦に4個,横に4個の等間隔に並んだ16個の点があり,縦横に隣り合う点どうしの距離は2cmである。これらの点の中からいくつかの点を選び,選んだ点どうしを結んでできる図形について(1) 面積が8cm2の正方形は全部で何個できるか。 ・1辺2√2cm(赤)…4個 (右上図参照) (2) 正方形は全部で何個できるか。 ・1辺2cm…3×3＝9個 ・1辺4cm…2×2＝4個 ・1辺6cm…1個 ・1辺2√2cm(赤)…4個 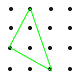 ・1辺2√5cm(青)…2個よって,9＋4＋1＋4＋2＝20個 (3) 面積が10cm2の直角三角形は全部で何個できるか。 ・等辺2√5cmの直角二等辺三角形(緑)…16個 |
0,1,2,3,4,5を並べて3桁の整数 をつくる。 (1) 桁の整数は何個あるか求めよ。 【解】百位は0以外 (6−1)×(6−1)×(6−2)＝5×5×4＝100個 (2) 430以上の整数は何個あるか求めよ。 【解】 ・430〜453…1×2×(6−2)＝2×4＝8 ・501〜543…1×5×(6−2）＝5×4＝20 全部で,8＋20＝28個 (3) 6の倍数は何個あるか求めよ。 【解】一位は0,2,4で,各位の和は3の倍数 ・一位が0…(十,百)＝(1,2) (1,5) (2,4) (4,5) ・一位が2…(十,百)＝(0,1) (0,4) (1,3) (2,5) ・一位が4…(十,百)＝(0，2) (0,5) (2,3) (3,5) 全部で,8＋6＋6＝20個 |
|||||||||||||
| ２ | 立命館守山高校 （Ｒ４年） ★★★ | ５ | 大阪教育大附属平野学舎 （Ｒ４年） ★★★ | |||||||||||
| できる整数のうち,最も小さい数をNとする。 (1) Nが奇数となる場合は全部で何通りあるか。 【解】一位は1,5,7かつ,各位が昇順 ・一位が1…なし ・一位が5…1245 ・一位が7…1247,1257,1457,2457 全部で,0＋1＋4＝5通り (2) Nが3の倍数となる場合は全部で何通りあるか。 【解】(3で割ると余り1)×2＋(3で割ると余り1)×2 つまり,(1,4,7から2つ選ぶ)と(2,5,8から2つ選ぶ) 全部で,3×3＝9通り (3) Nが2000より小さくなる場合は全部で何通りあるか。 【解】千位は1 (2,4,5,7,8)の5つから3つ選ぶ＝5つから2つ選ぶ
|
分ける方法は,それぞれ何通りあるか。 (1) A,B,Cの3人に分ける場合。 【解】分ける本数で場合分け ・(0,0,4)…3通り ・(0,1,3)…6通り ・(0,2,2)…3通り ・(1,1,2)…3通り 全部で,3＋6＋3＋3＝15通り (2) 区別のつかない3つのカゴに分ける場合。 【解】どの場合も1通りで, 4通り (3) 各バナナに異なるシールをはって3つのカゴに分ける場合。 【解】バナナをａｂｃｄとすると ・(abcd,,0,0)…1通り ・(abc,d,0) (abd,c,0) (acd,b,0) (acd,b0) (bcd,a,0)…4通り ・(ab,cd,0) (ac,bd,0) (ad,bc,0)…3通り ・(ab,c,d) (ac,b,d) (ad,b,c) (bc,a,d) (bd,a,c) (cd,a,b)…6通り 全部で,1＋4＋3＋6＝14通り |
|||||||||||||
| ３ | 慶應義塾志木高校 （Ｒ６年） ★★★ | ６ | 早大本庄高等学院 （Ｒ６年） ★★★ | |||||||||||
 ↑と→の２種類の矢印を左から順に並べてそれに従いＡ地点からマス目状の道を１つずつ進んでいく。(1) ,B地点にたどり着いた。並べ方は何通りか。 【解】計7枚のうち,↑3枚を並べる方法
【解】9枚目までで,PかQに到着 ・Pに到着…↑6枚と→3枚を並べる方法
|
すべてのマス目に次の【ルール】にしたがって自然数を入れる。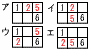 (1) 1と6がすでに入っているとき【解】2と5の入れ方は4パターン 残り3と4の入れ方はア〜エで, 1＋2＋1＋1＝5通り  (2) 1と4と8がすでに入っているとき,【解】2と7の入れ方は4パターン 残り3,5,6の入れ方はア〜エで, 1＋1＋1＋1＝4通り 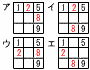 (3) 1と5と9がすでに入っているとき,【解】2と8の入れ方は4パターン 残り3,4,6,7の入れ方はア〜エで, 2＋3＋3＋4＝12通り |
|||||||||||||