 データの活用 |
１１ 集合とベン図 （略解） |
| データの活用 |
１１ 集合とベン図 （略解） |
| １ | 法政大第二高校 （Ｒ３年） ★★ | ５ | 帝塚山学院泉ヶ丘高校 （Ｒ５年） ★ | ||||
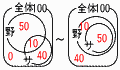 100人の生徒に対して,野球とサッカーのどちらが好きかを調査したところ,野球が好きな生徒は60人,サッカーが好きな生徒は50人であった。このとき,「野球もサッカーもどちらも好き」と回答した生徒の人数は何人以上何人以下と考えられるか,答えなさい。【解】図で重なり具合をみる ・左の場合(重なりが少ない) 最小値＝(60＋50)−100＝10人 ・右の場合(重なりが多い) 最大値(サッカー好きが全員,野球も好き)＝50人 よって, 10人以上,50人以下 |
ある高校で全校生徒を対象に,夏休みにどこへ旅行したか調査を行った。 その結果,国内旅行に行った生徒は全体の30％,海外旅行に行った生徒は全体の15％,国内旅行にも海外旅行にも行った生徒は全体の2％であった。 また,国内旅行にも海外旅行にも行かなかった生徒は513人であった。 この高校の全校生徒の人数を求めなさい。 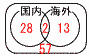 【解】(右図参照) どちらも行かなかった生徒は 100−{(30＋15)−2}＝100−43＝57％ 513÷0.57＝900人 |
||||||
| ２ | 宇都宮短大附属高校 （Ｒ４年） ★ | ６ | 筑波大附属坂戸高校 （Ｒ６年） ★ | ||||
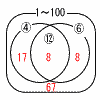 100以下の自然数のうち,4の倍数であるが6の倍数でないものは全部で[ ]個ある。【解】4と6の最小公倍数は12 12の倍数…100÷12＝8個 4の倍数 …100÷4＝25個 6の倍数 …100÷6＝16個 25−8＝17個 |
 次のア〜オのことがらのうち,それぞれ正しいものには〇,正しくないものには×と答えなさい。【解】 ア 正方形ならば長方形 〇 イ ひし形ならば平行四辺形 〇 ウ ひし形ならば正方形 × エ 長方形ならば平行四辺形 〇 オ 長方形ならばひし形 × |
||||||
| ３ | 大阪星光学院高校 （Ｒ６年） ★★ | ７ | 慶應義塾志木高校 （Ｒ３年） ★★ | ||||
| ある工場では２種類の製品A,Bを生産しており,製品A,Bの個数の比は7:6である。また,それぞれの不良品の個数の比は5:3であり,不良品でないものの個個の比は9:8である。 製品Ａについて,不良品と不良品でないものの個数の比を最も簡単な整数の比で表すと[ ]である。 
 zよって,5y:9z＝(5× z):9z＝10:81 |
 ある文房具店に鉛筆とボールペンがあり,その本数の比は6:5である。また,黒の鉛筆と黒のボールペンの本数の比は5:3で,黒以外の鉛筆と黒以外のボールペンの本数の比は8:7である。このとき,次の問いに答えよ。(1) 鉛筆のうち,黒と黒以外の本数の比 【解】右上図参照 (鉛):(ボ)＝(5x＋8y):(3x＋7y)＝6:5 5(5x＋8y)＝6(3x＋7y)より,y＝  x(鉛黒):(鉛外)＝5x:8y＝5x:(8× x)＝5:28(2) ボールペンの全本数が400本より多く450本より少ないとき,鉛筆の全本数 【解】 (ボ)＝3x＋7y＝3x＋(7× x)＝ x（xは偶数）800＜ x＜900より,14.5＜x＜16.4x＝16で,(鉛)＝5x＋8y＝33x＝33×16＝528本 |
||||||
| ４ | 滋賀県立高校 （Ｒ４年） ★ | ||||||
| 3,4,5,6,7の数字が書かれたカードが1枚ずつある。この5枚のカードから同時に2枚のカードを引くとき,2枚のカードの数字の積が2の倍数でなく,3の倍数でもない確率を求めなさい。ただし,どのカードを引くことも同様に確からしいとします。 【解】 5枚から2枚の引き方は,5×4÷2＝10通り 2,3の倍数でないのは,5×7だけで, 確率＝  |
|||||||
