 データの活用 |
１３ 数列２ （略解） |
| データの活用 |
１３ 数列２ （略解） |
| １ | 岡山白陵高校 （Ｒ３年） ★★ | ５ | 京都府立高校 （Ｒ４年） ★★ | ||||||||
| 32021の一の位を求めよ。 【解】31＝3,32＝9,33＝27,34＝81,35＝243,36＝729… 一位を並べると,3971,3971,…(4乗周期) 2021÷4＝505余り1で, 3 |
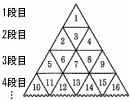 同じ大きさの正三角形の板がたくさんある。(1) 7段目の左端の正三角形の板に書かれている数と7段目の右端の正三角形の板に書かれている数をそれぞれ求めよ。 【解】n段目の右端はn2 7段目の左端は,62＋1＝37 7段目の右端は,72＝49 (2) n段目の左端の正三角形の板に書かれている数とn段目の右端の正三角形の板に書かれている数の和が1986であった。このとき,nの値を求めよ。 【解】 (n−1)2＋1＋n2＝1986 n2−n−992＝0 (n＋31)(n−32)＝0より, n＝32 |
||||||||||
| ２ | 明治学院東村山高校 （Ｒ４年） ★★ | ||||||||||
| 以下のように規則的に数が並んでいるとき, 2,|4, 4,|6, 6, 6,|8, 8, 8, 8,|10, 10, 10, 10, 10,|12, … (1) 21番目までのすべての数の和 【解】1＋2＋…＋6＝21で,6群の最後の項 和＝2＋4×2＋6×3＋…＋12×6 ＝2＋8＋18＋32＋50＋72＝182 (2) 50番目の数 【解】1＋2＋…＋9＝45で,10群 10×2＝20 (3) 100を初めて超えるのは,何番目の数か 【解】100が50個並ぶのは50群 1＋2＋…＋50＝  ×50×51＝1275番目1275＋1＝1276番目 |
|||||||||||
| ３ | 尚絅学院高校 （Ｒ４年） ★★ | ６ | 近畿大附属豊岡高校 （Ｒ５年） ★ | ||||||||
【解】各組の先頭は1,3,5,7,9,11,13,15,17,19,… よって,15＋16＋17＝48 (2) n番目の3つの数の和をnを用いて表しなさい。 【解】各組の先頭は奇数 n番目の組では,(2n−1)＋2n＋(2n＋1)＝6n (3) 6の数のうち最も小さい数を求めなさい。 【解】n番目と(n＋1)番目で,和＝6n＋6(n＋1)＝486 12n＝486−6で,n＝40 2n−1にn＝40を代入して,2×40−1＝79 |
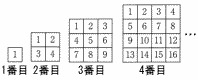 正方形のカードを図のように並ぺる。(1) nは2以上の自然数とする。n番目で左下の隅にあるカードに書かれた数をnの式で表しなさい。 【解】右下の数より(n−1)小さいから, n2−(n−1)＝n2−n＋1 (2) n番目で,四隅の4つの数の和が394になるとき,nの値 【解】左上＝1, 右上＝n, 左下＝n2−n＋1, 右下＝n2 1＋n＋(n2−n＋1)＋n2＝394 2n2＋2＝394で, n＝14 |
||||||||||
| ４ | 常盤高校 （Ｒ６年） ★ | ７ | 宇都宮短大附属高校 （Ｒ６年） ★★ | ||||||||
 正方形の白板と黒板を図のように規則的に増やしていく。(1) 6段のとき,白板は[ ]枚である。 【解】白は3枚ずつ増えて, 5,8,11,14,17 (2) n段のとき,白板は[ ]枚である。ただし,nを使った最も簡単な式で表せ。 【解】5＋3(n−2)＝3n−1 (3) 白板がちょうど26枚のとき,黒板は[ ]枚である。 【解】3n−1＝26より,n＝9段 よって, (9−1)2＝64 |
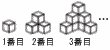 立方体をつなぎ合わせて立体をつくる。(1) 4番目の立体で,見えないブロックの個数 【解】奥の縦で, 3個 (2) n番目の立体で,見えないブロックの個数をnを用いて表せ。 【解】奥の縦はn個だから, n−1個 (3) 4番目の立体に使われているブロックの個数を求めよ。 【解】1＋3＋5＋7＝16個 (4) n番目の立体のプロックの個数をnを用いて表せ。 【解】1,4,9,16,…, n2個 (5) ブロックが2024個あるとき,最も大きい立体は[A ]番目の立体であり,このときプロックは[B ]個あまる。 【解】n2＜2024より, n＝44番目 2024−442＝88個 |
||||||||||