 データの活用 |
１３ 数列２ | 月 日（ ） |
| データの活用 |
１３ 数列２ | 月 日（ ） |
| １ | 岡山白陵高校 （Ｒ３年） ★★ | ５ | 京都府立高校 （Ｒ４年） ★★ | ||||||||
| 32021の一の位を求めよ。 |
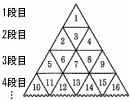 同じ大きさの正三角形の板がたくさんある。これらの板を,重ならないようにすき間なくしきつめて,大きな正三角形を作り,上の段から順に1段目,2段目,3段目,…とする。右の図のように,1段目の正三角形の板には1を書き,2段目の正三角形の板には,左端の板から順に2,3,4を書く。3段目の正三角形の板には,左端の板から順に5,6,7,8,9を書く。4段目以降の正三角形の板にも同じように,連続する自然数を書いていく。たとえば,4段目の左端の正三角形の板に書かれている数は10であり,4段目の右端の正三角形の板に書かれている数は16である。(1) 7段目の左端の正三角形の板に書かれている数と7段目の右端の正三角形の板に書かれている数をそれぞれ求めよ。 (2) 段目の左端の正三角形の板に書かれている数とn段目の右端の正三角形の板に書かれている数の和が1986であった。このとき,nの値を求めよ。 |
||||||||||
| ２ | 明治学院東村山高校 （Ｒ４年） ★★ | ||||||||||
| 以下のように規則的に数が並んでいるとき, 2, 4, 4, 6, 6, 6, 8, 8, 8, 8, 10, 10, 10, 10, 10, 12, … (1) 21番目までのすべての数の和を求めなさい。 (2) 50番目の数を求めなさい。 (3) 100を初めて超えるのは,何番目の数か求めなさい。 |
|||||||||||
| ３ | 尚絅学院高校 （Ｒ４年） ★★ | ６ | 近畿大附属豊岡高校 （Ｒ５年） ★ | ||||||||
下のように規則的に３つの数の組を作ります。このとき,左から1番目の組,2番目の組,3番目の組,……と呼ぶことにします。
(2) n番目の組について,3つの数の和をnを用いて表しなさい。 (3) 連続した2つの組について,6つの数の和が486になるとき,6の数のうち最も小さい数を求めなさい。 |
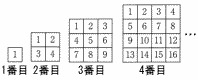 自然数が書かれた正方形のカードを図のように縦と横が同じ枚数となるように,左上から小さい数順に並ぺる。(1) nは2以上の自然数とする。n番目で左下の隅にあるカードに書かれた数をnの式で表しなさい。 (2) n番目で,四隅の4つの数の和が394になるとき,nの値を求めなさい。 |
||||||||||
| ４ | 常盤高校 （Ｒ６年） ★ | ７ | 宇都宮短大附属高校 （Ｒ６年） ★★ | ||||||||
 正方形の白板と黒板を図のように規則的に増やしていく。(1) 6段のとき,白板は[ ]枚である。 (2) n段のとき,白板は[ ]枚である。ただし,nを使った最も簡単な式で表せ。 (3) 白板がちょうど26枚のとき,黒板は[ ]枚であ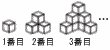る。 |
 図のように,同じ大ききの立方体のブロックをある規則にしたがってすき間なくつなぎ合わせて立体をつくる。(1) 立体をつくるときに図の角度からは見えないブロックの個数を考える｡例えば,3番目の立体では見えないブロックは2個である。4番目の立体において,見えないブロックの個数を求めよ。 (2) n番目の立体において,見えないブロックの個数をnを用いて表せ。 (3) 4番目の立体に使われているブロックの個数を求めよ。 (4) n番目の立体に使われているプロックの個数をnを用いて表せ。 (5) ブロックが全部で2024個あるとき,それらを使ってつくりあげることができる最も大きい立体は[A ]番目の立体であり,このときプロックは[B ]個あまる。 |
||||||||||
