 データの活用 |
１４ 数列３ （略解） |
| データの活用 |
１４ 数列３ （略解） |
| １ | 静岡県立高校 （Ｒ６年） ★ | ５ | 日本大習志野高校 （Ｒ６年） ★ | |||||||||||||||||||||||||
【解】4行n列の数は8n よって, 3行n列の数は8n－2 |
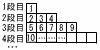 このとき,上から5段目の一番右にある自然数は[ ]であり,2024は上から[ ]段目の一番左から[ ]番目にある。【解】5段目の末項は52＝25 442＜2024＜452より,45段目(1936,1937,…,2025) 45段目には,45×2－1＝89項あって ,88番目 |
|||||||||||||||||||||||||||
| ２ | 群馬県立高校 （Ｒ５年） ★ | ６ | 早大高等学院 （Ｒ４年） ★★★ | |||||||||||||||||||||||||
整数a,bと5が,左から規則的に並んでいる。
【解】a, 5, b の繰り返し 20÷3＝6余り2 7群の2項目で, 5 (2) 7番目までの和が18, 50番目までの和が121のとき,aとbの値をそれぞれ求めなさい。 【解】 7番目までの和＝2(a＋5＋b)＋a＝18 3a＋2b＋10＝18…ア 50番目までの和＝16(a＋5＋b)＋(a＋5)＝121 17a＋16b＋85＝121…イ アイを連立させて解くと, a＝4, b＝－2 |
自然数nに対して,3nを7で割った余りをan 1段目 a1 2段目 a2 a3 3段目 a4 a5 a6 4段目 a7 a8 a9 a10 (1) 4段目に並ぶa7,a8,a9,a10の値 【解】3段目まで計算してみると,
(2) 2022段目に並ぶ数のうち,左端の数 【解】6で割ったときの余りで考える 1～2022段目の総個数＝1＋2＋…＋2022 ＝  ×2021×2022＝2021×1011＝(336×6＋5)(168×6＋3)＝(5余る)×(3余る) 2022段目の左端＝(5余る)×(3余る)＋1＝(16余る) ＝(6で割ると4余る)＝4 (3) 和が初めて2022より大きくなるとき,mを 【解】1周期の和＝3＋2＋6＋4＋5＋1＝21 2022＝21×96＋6で,mは96周期＋3 m＝6×96＋3＝579 (4) a2022を含む段に並ぶすべての数の和 【解】x段目までの総和＝ x(x＋1)＞2022x＝63のとき, x(x＋1)＝2016で,a2022は64段目64＝6×10＋4＝10周期の和＋4番目で a2017＋a2018＋…＋a2080 ＝21×10＋(3+2+6+4)＝210＋15＝225 |
|||||||||||||||||||||||||||
| ３ | 玉川学園高校 （Ｒ４年） ★★★ | |||||||||||||||||||||||||||
 黒い石を,図のように並べていく。(1) n回目の一番下の段の石の個数を求めよ。 【解】最下段は偶数列 n×2＝2n個 (2) n回目の石の個数を求めよ。 【解】ｎが偶数のとき,(奇数も同様)  (2＋2n)＋(4＋2n－2)＋…＝ n(2n＋2)＝n(n＋1)個, または(n2＋n)個(3) 石の個数が156個になるのは何回目か求めよ。 【解】n2＋n＝156より, (n＋13)(n－12)＝0で,n＝12回目 |
||||||||||||||||||||||||||||
| ４ | 大阪学院大高校 （Ｒ６年） ★ | ７ | 青山学院高等部 （Ｒ６年） ★★ | |||||||||||||||||||||||||
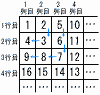 次の図のように,連続する自然数を1から順に規則的に並べていく。(1) 6 行目の1列目の数を答えなさい。 【解】62＝36 (2) 9行目の9列目の数を答えなさい。 【解】92－8＝73 (3) n行目のn列目の数をnを用いて表しなさい。 【解】n2－(n－1)＝n2－n＋1 ((4) 101行目の100列目の数を答えなさい。 【解】1012－99＝10201－99＝10102 |
0,1,2,3,4の5種類の数字を用いて作られる正の整数を考える。ただし,同じ数字を繰り返し用いてよいこととする。 これらを小さい方から順に並べると, 1,2,3,4,10,11,12… となる。 (1) 小さい方から数えて24番目の数を求めよ。 【解】1,2,3,4❘10,11,12,13,14❘…❘40,41,42,43,44❘100… 1＋(24－4)÷5＝5だから,5群の末項で, 44 (2) 2024は小さい方から数えて何番目の数か答えよ。 【解】2024(5)＝2×53＋2×5＋4＝264番目 |
|||||||||||||||||||||||||||