データの活用	１５　さいころ１　（略解）
以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。

１	芝浦工大附属高校　（Ｒ５年）　★	６	成蹊高校　（Ｒ５年）　★
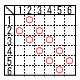大小2個のさいころを同時に投げるとき,出た目が連続する2つの整数となる確率を求めなさい。 【解】表より,10通り 　10÷36＝5/18		十の位の数がa,一の位の数がbである2桁の整数が6の倍数となる確率を求めよ。 【解】12,24,36,42,54,66の6通り 　6÷36＝
２	都立立川高校　（Ｒ４年）　★	７	都立墨田川高校　（Ｒ４年）　★
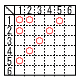1から6までの目が出るさいころを2回投げる。1回目に出た目の数をa,2回目に出た目の数をbとするとき,337(a＋b)が2022の約数となる確率を求めよ。 【解】2022＝337×6 a＋b＝1,2,3,6の場合の8通りで,　8÷36＝		1から6までの目が出る大小1つずつのさいころを同時に1回投げる。大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとするとき,a≧3bとなる確率を求めよ。 【解】aと3bの表にまとめると5通りで,
３	立命館慶祥高校　（Ｒ４年）　★★★	８	青雲高校　（Ｒ４年）　★★★
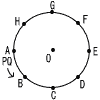図のように,円Oの周上に8点A,B,C,D,E,F,G,Hが等間隔に並んでいる。 (1) 点Pが頂点Eにあり,点Qが頂点Dにあるようなさいころの目の出方は何通りあるか,求めなさい。 【解】Pより,大は2か6 P 1 2 3 4 5 6 C E G A C E Q 1 2 3 4 5 6 1 C D E F G H 2 D E F G H A 3 E F G H A B 4 F G H A B C 5 G H A B C D 6 H A B C D E (大,小)＝(2,3),(6,5)の 2通り (2) 2点P,Qが同じ頂点にある確率を求めなさい。 【解】大をx,小をyとすると, 2x＝x＋yより,x＝y (大小同じ目) 　6÷36＝ (3) 3点B,P,Qを結んだとき,△PBQが直角三角形となる確率を求めなさい。 【解】 直角三角形となるのは右表の赤字で,8通り 　8÷36＝		(1) 　3 ＋ 2 の値が整数となる確率を求めよ。 　a b 【解】(a,b)＝(1,1) (1,2) (2,4) (3,1) (3,2) (4,6) 　　 (5,5) の7通り　　確率＝7÷36＝7/36 (2) a＋b＋cが奇数になる確率を求めよ。 1 2 3 4 2 3456 3 456 456 4 56 56 56 5 5 6 6 6 【解】和の確率は,奇数も偶数も同じで, (3) a＜b＜cとなる確率を求めよ。 【解】3つの場合でもサイコロ表を cが右表の値のときで,20通り 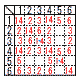確率＝ 20 ＝ 5 216 54 (4) √abcが整数となる確率を求めよ。 【解】積abcが平方数より, 　cが右表の値のときで,38通り 確率＝ 38 ＝ 19 216 108
４	桜美林高校　（Ｒ６年）　★	９	盈進高校　（Ｒ６年）　★★
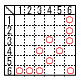図のような,1から6までの番号が書かれた6個のマスがある。大小2つのさいころを同時に投げ,まず,大きいさいころの出た目の数の約数が書かれたマスに〇をつけ,次に,小さいさいころの出た目の数の約数が書かれたマスのうち,まだ〇がつけられていないマスに〇をつける。このとき,4個のマスに〇がつけられている確率を求めなさい。 【解】 表より,11通りで,11/36		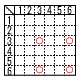1回目,2回目に出た目をそれぞれa,bとする。 (1) aとbがともに3の倍数である確率 【解】 右表より4通りで, (2) 和a＋bが3の倍数である確率を求めなさい。 【解】右下表より12通りで, 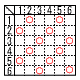(3) ab＋cが3の倍数である確率を求めなさい。 【解】3の剰余系で3パターン ・ab＝3,6,9,12,15,18,24,30,36 　　　　　　　　　　かつ,c＝3,6の場合 　　(2＋4＋1＋4＋2＋2＋2＋2＋1)×2＝40通り ・ab＝1,4,10,16,25かつ,c＝2,5の場合 　　(1＋3＋2＋1＋1)×2＝16通り ・ab＝2,5,8,20かつ,c＝1,4の場合 　　(2＋2＋2＋2)×2＝16通り 全部で,40＋16＋16＝72通り　　よって, 72÷63＝
５	国立音大附属高校　（Ｒ６年）　★
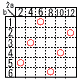大小2個のさいころを同時に投げて,大きいきいころの出た目をa,小さいさいころの出た目をbとする。このとき,2a＋bの値が7の倍数となる確率を求めなさい。 【解】 表より6通りで,

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難