 データの活用 |
１５ さいころ (確率) １ | 月 日（ ） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | ||
| データの活用 |
１５ さいころ (確率) １ | 月 日（ ） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | ||
| １ | 芝浦工大附属高校 （Ｒ５年） ★ | 6 | 成蹊高校 （Ｒ５年） ★ | |||||||
| 大小2個のさいころを同時に投げるとき,出た目が連続する2つの整数となる確率を求めなさい。 |
大小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。十の位の数がa,一の位の数がbである2桁の整数が6の倍数となる確率を求めよ。 |
|||||||||
| ２ | 都立立川高校 （Ｒ４年） ★ | 7 | 都立墨田川高校 （Ｒ４年） ★ | |||||||
| 1から6までの目が出るさいころを2回投げる。1回目に出た目の数をa,2回目に出た目の数をbとするとき,337(a＋b)が2022の約数となる確率を求めよ。 |
1から6までの目が出る大小1つずつのさいころを同時に1回投げる。大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとするとき,a≧3bとなる確率を求めよ。 |
|||||||||
| ３ | 立命館慶祥高校 （Ｒ４年） ★★★ | 8 | 青雲高校 （Ｒ４年） ★★★ | |||||||
図のように,円Oの周上に8点A,B,C,D,E,F,G,Hが等間隔に並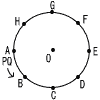 んでいる。大小2つのさいころを同時に1回投げ,点Pは頂点Aから大きいさ いころの出た目の数の2倍だけ,時計の針と反対の方向に頂点を移動する。また,点Qは頂点Aから大小2つのさいころの出た目の数の和だけ,点Pと同じ方向に頂点を移動する。(1) 点Pが頂点Eにあり,点Qが頂点Dにあるようなさいころの目の出方は何通りあるか,求めなさい。 (2) 2点P,Qが同じ頂点にある確率を求めなさい。 (3) 3点B,P,Qを結んだとき,△PBQが直角三角形となる確率を求めなさい。 |
3個のさいころA,B,Cを同時に１回投げる。Aの出た目の教をa,Bの出た目の数をb,Cの出た目の数をcとする｡
(2) a＋b＋cが奇数になる確率を求めよ。 (3) a＜b＜cとなる確率を求めよ。 (4) √abcが整数となる確率を求めよ。 |
|||||||||
| ４ | 桜美林高校 （Ｒ６年） ★ | 9 | 盈進高校 （Ｒ６年） ★★ | |||||||
 図のような,1から6までの番号が書かれた6個のマスがある。大小2つのさいころを同時に投げ,まず,大きいさいころの出た目の数の約数が書かれたマスに〇をつけ,次に,小さいさいころの出た目の数の約数が書かれたマスのうち,まだ〇がつけられていないマスに〇をつける。このとき,4個のマスに〇がつけられている確率を求めなさい。 |
1個のさいころを2回投げる。1回目,2回目に出た目をそれぞれa,bとする。 (1) aとbがともに3の倍数である確率を求めなさい。 (2) 和a＋bが3の倍数である確率を求めなさい。 (3) さらにもう1度さいころを投げて出た目をcとする。このとき,式ab＋cが3の倍数である確率を求めなさい。 |
|||||||||
| 5 | 国立音大附属高校 （Ｒ６年） ★ | |||||||||
| 大小2個のさいころを同時に投げて,大きいさいころの出た目をa,小さいさいころの出た目をbとする。このとき,2a＋bの値が7の倍数となる確率を求めなさい。 |
||||||||||
