 データの活用 |
１７ さいころ (確率) ３ （略解） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | |
| データの活用 |
１７ さいころ (確率) ３ （略解） |
| 以下の問題では,さいころは,どの目が出ることも同様に確からしいものとします。 | |
| １ | 桜美林高校 （Ｒ４年） ★★ | ５ | 京都府立高校 （Ｒ４年） ★★ | ||||||||||||||
 大きいさいころをa,小さいさいころをb(1)  ＞ となる確率【解】b＞ aより,サイコロ表を作る表より26通りで, 確率＝26÷36＝13/18 (2) a＜b＜2aとなる確率を求めなさい。 【解】 (a,b)＝(2,3) (3,4) (3,5) (4,5) (4,6) (5,6)の6通り 確率＝6÷36＝  |
1から6までの目があるさいころを2回投げ,1回目に出た目の数をa,2回目に出た目の数をbとする。 (1)  ＝2 となる確率を求めよ。 【解】(a,b)＝(2,1) (4,2) (6,3)の3通りで, 確率＝3÷36＝  (2) の値が循環小数になる確率を求めよ。【解】既約分数ならbは2,5以外の素数で3 表(〇)より8通りで, 確率＝8÷36＝  |
||||||||||||||||
| ２ | 桐光学園高校 （Ｒ４年） ★★★ | ６ | 灘 高校 （Ｒ４年） ★★★ | ||||||||||||||
| 大中小の3個のさいころを投げ,目の積を考える。 (1) 出た目の数の積が5の倍数となる確率 【解】1－(5が出ない確率) 確率＝1－(  )3＝91/216(2) 出た目の数の積が8の倍数となる確率 【解】 ・(偶数が3個)…(  )3＝ ・(4が2個)と(奇数1個)…(  )2××3＝ ・(4が1個)と(2か6)と(奇数1個)… × ××6＝確率＝ ＋＋＝ |
ただ1つの解をもつ確率は[ア ]で,異なる2つの整数の解をもつ確率は[イ ]である。 【解】 (ア) ただ1つの重解 ・x2－ax＋b＝(x－1)2のとき,a＝2,b＝1 ・x2－ax＋b＝(x－2)2のとき,a＝4,b＝4 (a,b)＝(2,1) (4,4)の2通りで,ア＝2÷36＝  (イ)異なる2整数解 ・x2－ax＋b＝(x－1)(x－2), (x－1)(x－3), (x－1)(x－4), (x－1)(x－5), (x－2)(x－3) の5通りで，イ＝5÷36＝  |
||||||||||||||||
| ３ | 四天王寺高校 （Ｒ５年） ★★ | ７ | 東海大付属浦安高校 （Ｒ４年） ★★ | ||||||||||||||
| Aの出た目の数をa,Bの出た目の数をbとします。 (1) √ab＜5をみたす確率 【解】ab＜25で, (a,b)≠(5,5) (5,6) (6,5) (6,6) 32通りで, 確率＝32÷36＝ 
確率＝3÷36＝
確率＝8÷36＝ |
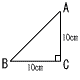 大きいサイコロの出た目の数をa,小さいサイコロの出た目の数をbとします。(1) CD＝CEとなる確率は[ ] 【解】 10－a＝bより,a＋b＝10 (a,b)＝(4,6) (5,5) (6,4) の3通り 確率＝3÷36＝ (2) △DCEの面積が10cm2となる確率は[ ] 【解】 △DCE＝ (10－a)b＝10より,(10－a)b＝20(10-a,b)＝(4,5) (5,4)で, (a,b)＝(6,5) (5,4) の2通り 確率＝2÷36＝ |
||||||||||||||||
| ４ | 駿台甲府高校 （Ｒ６年） ★★ | ８ | 明治学院高校 （Ｒ６年） ★★ | ||||||||||||||
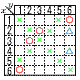 1から6までの目が出るさいころ1個を2回投げて,1回目に出た目をx,2回目に出た目をyとする。(1) xy＝6となる確率を求めよ。 【解】表(〇)より4通りで,確率＝  (2) x2－xy＋8＝0となる確率を求めよ。 【解】式変形して,y＝x＋  表(△)より2通りで,確率＝ (3) x2－6x＝y2－6yとなる確率を求めよ。 【解】式変形して,(x－y)(x＋y－6)＝0 x＝yまたはx＋y＝6を満たすのは表(×)で,確率＝5/18 |
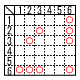 2つのさいころA,Bを同時に１回投げて,出た目をそれぞれa,bとする。a,bの最小公倍数をＸとするとき,(１) Ｘ＝6となる確率を求めよ。 【解】表(〇)より9通りで,確率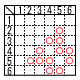＝   (2) Ｘ＞6となる確率を求めよ。 【解】表(〇)より12通りで,確率＝ |
||||||||||||||||
