| 17 さいころ (確率) 3 | 月 日( ) | |
| 以下の問題では,さいころはどの目が出ることも同様に確からしいものとします。 | ||
| 17 さいころ (確率) 3 | 月 日( ) | |
| 以下の問題では,さいころはどの目が出ることも同様に確からしいものとします。 | ||
| 1 | 桜美林高校 (R4年) ★★ | 5 | 京都府立高校 (R4年) ★★ | ||||||||||||||
| 大小2つのさいころを同時に投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとするとき, (1) (2) a<b<2aとなる確率を求めなさい。 |
1から6までの目があるさいころを2回投げ,1回目に出た目の数をa,2回目に出た目の数をbとする。 (1) (2) |
||||||||||||||||
| 2 | 桐光学園高校 (R4年) ★★★ | 6 | 灘 高校 (R4年) ★★★ | ||||||||||||||
| 大中小の3個のさいころを同時に投げ,出た目の数の積を考える。 (1) 出た目の数の積が5の倍数となる確率を求めよ。 (2) 出た目の数の積が8の倍数となる確率を求めよ。 |
サイコロAとサイコロBを投げ,Aの出た目の数をa,Bの出た目の数をbとする。xの2次方程式x2-ax+b=0がただ1つの解をもつ確率は[ア ]であり,この方程式が異なる2つの整数の解をもつ確率は[イ ]である。 |
||||||||||||||||
| 3 | 四天王寺高校 (R5年) ★★ | 7 | 東海大付属浦安高校 (R4年) ★★ | ||||||||||||||
| 2個のさいころA,Bを投げます。さいころAの出た目の数をa,さいころBの出た目の数をbとします。 (1) √ab<5をみたす確率を求めなさい。
|
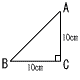 図のように,直角三角形ABCがあり,AC=BC=10cm,∠ACB=90°とします。大小2つのサイコロを同時に投げ,大きいサイコロの出た目の数をa,小さいサイコロの出た目の数をbとします。辺BC上に点Bからacmのところに点Dをとり,辺AC上に点Cからbcmのところに点Eをとります。 図のように,直角三角形ABCがあり,AC=BC=10cm,∠ACB=90°とします。大小2つのサイコロを同時に投げ,大きいサイコロの出た目の数をa,小さいサイコロの出た目の数をbとします。辺BC上に点Bからacmのところに点Dをとり,辺AC上に点Cからbcmのところに点Eをとります。(1) CD=CEとなる確率は[ ]となります。 (2) △DCEの面積が10cm2となる確率は[ ]となります. |
||||||||||||||||
| 4 | 駿台甲府高校 (R6年) ★★ | 8 | 明治学院高校 (R6年) ★★ | ||||||||||||||
| 1から6までの目が出るさいころ1個を2回投げて,1回目]に出た目をx,2回目に出た目をyとする。 (1) xy=6となる確率を求めよ。 (2) x2-xy+8=0となる確率を求めよ。 (3) x2-6x=y2-6yとなる確率を求めよ。 |
2つのさいころA,Bを同時に1回投げて,出た目をそれぞれa,bとする。a,bの最小公倍数をXとするとき, (1) X=6となる確率を求めよ。 (2) X>6となる確率を求めよ。 |
||||||||||||||||