４１８カード１（解答）

データの活用	１８　カード (確率) １　（略解）
以下の問題では,どのカードが引かれることも同様に確からしいものとします。

１

弘前聖愛高校　（Ｒ６年）　★

５

都立国立高校　（Ｒ４年）　★★

　1から6までの数字が書かれた6枚のカードが箱の中に入っている。このカードをよくまぜてから同時に2枚取り出し,小さい方の数字をa,大きい方の数字をbとする。このとき,√3×a×bが整数になる確率を求めなさい。
【解】3ab＝9,36すなわち,ab＝3,12
a＜bより,(a,b)＝(1,3) (2,6) (3,4) の3通り
取り出し方は全部で,6×5÷2＝15通りで, 確率＝

　10a＋bが3の倍数となる確率

【解】10a＋b＝3・3a＋(a＋b)
a＋bが3の倍数であればよい
(a,b)＝(1,2) (1,5) (2,4) (1,8) (2,7) (3,6)
　 (4,5) (4,8) (5,7)(7,8) は逆も含めて20通り
(a,b)＝(3,3) (6,6) の2通り
確率＝(20＋2)÷8²＝11/32

２

東洋大京北高校　（Ｒ４年）　★★★

６

夙川高校　（Ｒ４年）　★★

　箱の中に,2,3,5,10が1つずつ書かれたカードがあります。
(1) 和が12以下になる確率
【解】
4枚から2枚取るのは,4×3÷2＝6通り
和が12以下は,(2,3) (2,5) (2,10) (3,5)の4通り
確率＝4÷6＝

(2) 和が12以下が,2通りになるxの値
【解】10以外の4数から,和が12以下の3数を選ぶ
x＝1のとき,(1,2,3,5)→(1,2,3) (1,2,5) (2,3,5)
x＝4のとき,(,2,3,4,5)→(2,3,4) (2,3,5) (2,4,5) (3,4,5)
x＝6のとき,(2,3,5,6)→(2,3,5) (2,3,6)2通り
x＝7のとき,(2,3,5,7)→(2,3,5) (2,3,7)2通り
x＝8のとき,(2,3,5,8)→(2,3,5)
x＝9のとき,(2,3,5,9)→(2,3,5)
　2通りになるのは,x＝6,7

　3枚取り出し,並べて整数Xをつくる。

（1）M＝0となる確率を求めなさい。
【解】
(5枚から3枚取る方法)＝(5枚から2枚取る方法)
　＝5×4÷2＝10通り
(0)1枚と(1,2,3,4)から2枚だから,

確率＝	4×3	÷10	＝	6	＝
	2			10

（2）S＝6となる確率を求めなさい。
【解】
和が6は,(0,2,4) (1,2,3) の2通り
確率＝2÷10＝

（3）M＝Sとなる確率を求めなさい。
【解】
(0,2,4)の1通りで,確率＝1÷10＝

３

東大寺学園高校　（Ｒ５年）　★★★

７

巣鴨高校　（Ｒ４年）　★★

　袋の中に,数字の１が書かれたカードが1枚,数字の2が書かれたカードが2枚,数字の3が書かれたカードが3枚入っている。この袋の中からカードを1枚ずつ2回取り出し,取り出されたカードの数字を取り出した順にa,bとする。このとき,a＋1がbの倍数である確率を求めよ。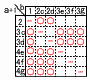

【解】取り出し方は全部で,6×5＝30通り
右表(〇)より,19通りで,確率＝19/30
　ただし,表(－)は1回目に取り出され済み

　和が7以下になる確率
【解】

6枚から3枚取る方法＝	6×5×4	＝20通り
	3×2×1

1が2枚あるから,
　・(1,1,2)1通り・(1,1,3)1通り・(1,1,4)1通り
　・(1,1,5)1通り・(1,2,3)2通り・(1,2,4)2通り
確率＝(1×4＋2×2)÷20＝8/20＝

４

都立新宿高校　（Ｒ６年）　★★

８

東北学院高校　（Ｒ６年）　★★

　箱の中に－2,－1,0,2,3,5の数字を1つずつ書いた6枚のカ一ド入っている。
　この箱の中にある６枚のカードから,カードを1枚取り出し,取り削したカードに書いてある数字をaとし,取り出したカードを箱の中に戻して,もう一度箱の中にある6枚

のカードから,カードを１枚取り出し,取り出したカードに書いてある数字をbとするとき, 4≦(a＋b)²≦16 となる確率を求めよ。
【解】a＋b＝±2,±3,±4となればよい
右表(〇)より,17通りで, 確率＝17/36

　7枚のカードをよく切ってから3枚同時にひき,小さい順にカードを並べます。
(1) ひいたカードに記入された数がすべて奇数である確率を求めなさい。

【解】	確率＝	₄Ｃ₃	＝	4･3･2	×	3・2・1	＝	4
	確率＝	₇Ｃ₃	＝	3・2・1	×	7・6・5	＝	35

(2) 2⃣,5⃣,7⃣のように隣り合うカードに記入された数の差がともに１より大きくなる確率を求めなさい。
【解】以下の10通りで, 確率＝10/35＝

135 136 137 146 147 157 246 247 257 357

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難