データの活用 ２０　カード (確率) ３　（略解）
以下の問題では,どのカードが引かれることも同様に確からしいものとします。
１ 日大明誠高校　（Ｒ４年）　★★ ５ 三重県立高校　（Ｒ４年）　★★★
(1) a＋bが24の約数になる確率は[　　]である。
【解】(a,b)の組合せを考える
・(1,1) (2,2) (3,3) (4,4) (6,6) が各1通り
・(1,2) (1,3) (1,5) (1,7) (2,4) (2,6) (3,5) (3,9)
　　　(4,8) (5,7) が各2通り
　確率＝(1×5＋2×10)÷92＝25/81
(2) √a×bが整数になる確率は[　　]である。
【解】(a,b)の組合せを考える
・(1,1) (2,2) … (9,9) が各1通り
・(1,4) (1,9) (2,8) (4,9) が各2通り
　確率＝(1×9＋2×4)÷92＝17/81		 　1⃣,2⃣,3⃣,4⃣,5⃣,6⃣…のように,1からnまでの自然数が順に1つずつ書かれたn枚のカードがある。
(1) n＝10のとき,√aが自然数となる確率
n 1 2 3 4 5 6 7 8 9 10 11 12
12 12
6		 12
6
4		 12
6
4
3		 12
6
4
3		 12
6
4
3
2		 12
6
4
3
2		 12
6
4
3
2		 12
6
4
3
2		 12
6
4
3
2		 12
6
4
3
2		 12
6
4
3
2
1
【解】
a＝1,4,9の3通り
確率＝3÷10＝
(2)確率がになるとき,nの値すべて
【解】a＝1,2,3,4,6,12の6通り　かつn≦12
の個数＝nになるのは, n＝10,12
２ 立教新座高校　（Ｒ４年）　★★ ６ 灘　高校　（Ｒ４年）　★★★
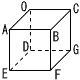　図のような立方体OABC-DEFGと,A,B,C,D,E,F,Gの文字が1つずつ書かれた7枚のカードが入った袋があります。この袋の中から同時に2枚のカードを取り出します。取り出したカードに書かれている文字と同じ文字の立方体の頂点を選び,その2点を通る直線をl とします。次の確率を求めなさい。

(1) 直線l と平面AEFBが垂直になる確率
【解】7点から2点の選び方＝7×6÷2＝21通り
垂直は,BC,ED,FGの3通り
　確率＝3÷21＝

(2) 直線l と直線OBがねじれの位置になる確率
【解】
ねじれの位置は,AD,AE,AF,AG,CD,CE,CF,CG,
　　DE,DG,EF,EG,FGの13通り
　確率＝13÷21＝13/21		 (1) ［PASS］という並びが含まれる確率
【解】全部の並べ方は,36通り
PASS〇〇, 〇PASS〇, 〇〇PASSの3パターン
　〇〇には,32＝9通りで, 確率＝(9×3）÷36＝
(2) 文字を9個並べたとき,
【解】先頭から初めてPASSが並ぶ場合分けで
ア PASS〇〇〇〇〇…35通り　　イ 〇PASS〇〇〇〇…35通り
ウ 〇〇PASS〇〇〇…35通り　　エ 〇〇〇PASS〇〇…35通り
オ 〇〇〇〇PASS〇…PASSPASS〇が
　　　アと重複するから,35－3＝3(34－1)通り
カ 〇〇〇〇〇PASS…PASS〇PASS, 〇PASSPASSが
　　　アイと重複するから,35－3×2＝3(34－2)通り
　確率＝ 35×4＋3(34－1)＋3(34－2) ＝ 35×6－9
39 39
　　＝ 32(27×6－1) ＝ 161 ＝ 161
39 37 2187
３ 大阪府立高校C　（Ｒ６年）　★★★ ７ 四天王寺高校　（Ｒ６年）　★★
　a＜c＜bである確率はいくらですか。
4 6 8
1 (8,14,5) (8,12,7) (8,10,9)
3 (6,14,7) (6,12,9) (6,10,11)
5 (4,14,9) (4,12,11) (4,10,13)
【解】
(a,b,c)のパターンは
　　右表のように9通り
このうち,a＜c＜bは5通り
　よって,確率＝
 　袋の中に,数字が1つずつ書かれた7枚のカードが入っています。1,3,5と書かれたカードは1枚ずつ,2,4と書かれたカードは2枚ずつ入っています。この袋からカードを1枚取り出すことを２回行います。

(1) Ｘ＝8になる確率を求めなさし
【解】7枚を, [ 1 2a 2b 3 4c 4d 5 ] と考える
取り出し方は全部で,7×6÷2＝21通り
このうち,キ＋キ＝8は, (3,5) の1通りで,確率＝1/21
(2) Ｘ＋Y＝9になる確率を求めなさい。
【解】キ＋グ＝9は, (4c,5) (4d,5) の2通りで,確率＝2/21
(3) Ｘ＞Yになる確率を求めなさい。
【解】
キ＞グは, (3,2a) (3,2b) (5,2a) (5,2b) (5,4c) (5,4d) の6通りで,
　確率＝6÷21＝
４ 灘　高校　（Ｒ５年）　★★★
　0点,1点,…,9点のうち,起こる確率が最も小さい得点は[　　]点であり,そのときの確率は[　　]である。
【解】 取り出し方は全部で,9Ｃ4＝ 9×8×7×6 ＝126通り
　 4×3×2×1
このうち,3数の和が10の倍数となるのは,次の8通り
　(1,2,7) (1,3,6) (1,4,5) (2,3,5) (3,8,9) (4,7,9) (5,6,9) (5,7,8)
5が最多出現だから,最小確率はa＝5点のときで,
　その確率＝4/126＝2/63

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難