データの活用	２０　カード (確率) ３	月　　　日（　　）
以下の問題では,どのカードが引かれることも同様に確からしいものとします。

１	日大明誠高校　（Ｒ４年）　★★	５	三重県立高校　（Ｒ４年）　★★★
1から9までの数字が書かれたカードが１枚ずつ入っている箱がA,Bの2箱ある。箱の中から1枚ずつカードを引き,箱Aから引いたカードをa,箱Bから引いたカードをbとする。 (1) a＋bが24の約数になる確率は[　　]である。 (2) √a×bが整数になる確率は[　　]である。		1⃣,2⃣,3⃣,4⃣,5⃣,6⃣…のように,1からnまでの自然数が順に1つずつ書かれたn枚のカードがある。このカードをよくきって１枚取り出すとき,取り出されたカードに書かれた自然数をaとする。 (1) n＝10のとき,√aが自然数となる確率を求めなさい。 (2) が自然数となる確率がになるとき,nの値をすべて求めなさい。
２	立教新座高校　（Ｒ４年）　★★	６	灘　高校　（Ｒ４年）　★★★
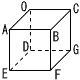図のような立方体OABC-DEFGと,A,B,C,D,E,F,Gの文字が1つずつ書かれた7枚のカードが入った袋があります。この袋の中から同時に2枚のカードを取り出します。取り出したカードに書かれている文字と同じ文字の立方体の頂点を選び,その2点を通る直線をl とします。次の確率を求めなさい。 (1) 直線l と平面AEFBが垂直になる確率 (2) 直線l と直線OBがねじれの位置になる確率		A,P,Sの3種類の文字から無作為に1文字を選ぶことを繰り返し行い,選んだ文字を選んだ順番に左から右に向かって1列に並べていく。 (1) 文字を6個並べたとき,［PASS］という連続した文字の並びが含まれる確率を求めよ。 (2) 文字を9個並べたとき,［PASS］という連続した文字の並びが含まれる確率を求めよ。
３	大阪府立高校C　（Ｒ６年）　★★★	７	四天王寺高校　（Ｒ６年）　★★
二つの箱A,Bがある。箱Aには奇数の書いてある3枚のカードが入っており,箱Bには偶数の書いてある3枚のカード4,6,8が入っている。A,Bそれぞれの箱から同時にカードを1枚ずつ取り出し,箱Aの中に残っている2枚のカードに書いてある数の和をa,箱Bの中に残っている2枚のカードに書いてある数の和をb,箱Aから取り出したカードに書いてある数と箱Bから取り出したカードに書いてある数との和をcとする。このとき,a＜c＜bである確率はいくらですか。		袋の中に,数字が1つずつ書かれた7枚のカードが入っています。1,3,5と書かれたカードは1枚ずつ,2,4と書かれたカードは2枚ずつ入っています。この袋からカードを1枚取り出すことを２回行います。 　ただし,取り出したカードは袋にもどしません。取り出したカードに書かれた数字のうち,奇数の和をＸ,偶数の和をYとします。 　例えば,取り出したカードに書かれた数字が1,2のときはＸ＝1,Y＝2になり,取り出したカードに書かれた数字が4,2のときはＸ＝0,Y＝6になります。 (1) Ｘ＝8になる確率を求めなさし (2) Ｘ＋Y＝9になる確率を求めなさい。 (3) Ｘ＞Yになる確率を求めなさい。
４	灘　高校　（Ｒ５年）　★★★
1から9までの数が書かれたカードが,それぞれ1枚ずつ合計9枚ある。この9枚のカードから4枚のカードを取り出す。取り出した4枚のうち,いずれか3枚に書かれている数の和が10の倍数になり,残りの１枚に書かれている数がaのとき,得点をa点とする。また,取り出した4枚のうち,どの3枚に書かれている数の和も10の倍数にならないとき,得点を0点とする。0点,1点,…,9点のうち,起こる確率が最も小さい得点は[　　]点であり,そのときの確率は[　　]である。

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用