データの活用	２３　玉　(確率)　３　（略解）
以下の問題では,どの玉が取り出されることも同様に確からしいものとします。

１	徳島県立高校　（Ｒ５年）　★★	５	法政大国際高校　（Ｒ４年）　★★
2個の玉の色が異なる確率を求めなさい。 【解】6個から2個の取り出し方は全部で,6×5÷2＝15通り 　・(赤,白)は,3×2＝6通り 　・(赤,青)は,3×1＝3通り 　・(白,青)は,2×1＝2通り よって, 確率＝ 6＋3＋2 ＝ 11 15 15		3個の中に白球が2個だけ入っている確率を求めよ。 【解】 6個から3個の取り方は,6C3＝ 6×5×4 ＝20通り 3×2×1 白3個から白2個の取り方は3通り 　・(白2,赤1)は,3×2=6通り 　・(白2,青1)は,3×1=3通り よって, 確率＝(6＋3)÷20＝9/20
２	山梨県立高校　（Ｒ６年）　★★	６	土浦日本大高校　（Ｒ５年）　★★
箱の中に,赤球2個,青球1個,白球2個が入っている。 【解】5個から2個の取り出し方は全部で,5×4÷2＝10通り 　・(青,赤)は,1×2＝2通り 　・(青,白)は,1×2＝2通り よって,確率＝(2＋2)÷10＝		3桁の整数で,奇数の確率は(　　)で,4の倍数の確率は(　　) 【解】取り出し方は全部で,33＝27通り ・奇数になるのは,一位が奇数のときだけ 　　3×3×2＝18通りで, 確率＝18÷27＝ ・4の倍数は, 　　112,132,212,232,312,332 の 6通りで,確率＝6÷27＝
３	お茶の水女子大附属高校　（Ｒ４年）　★★★	７	栃木県立高校　（Ｒ６年）　★★
袋の中に,赤玉,白玉,青玉の3色の玉が入っている。 (1) この袋から1つだけ玉を取り出すとき,白玉である確率を求めなさい。 【解】赤2k個,白3k個,青4k個とすると, 白玉の確率＝ 　　3k　　. ＝ 2k＋3k＋4k (2) mの値を求めなさい。 【解】各玉の確率が等しいから,各個数も等しい 　2k＋6(ア)＝3k＋m(イ)＝4k−2(ウ) ア＝ウより,k＝4 　これをイウに代入して,12＋m＝16−2 　m＝14−12＝2		袋の中に,1から5までの数字の玉が入っている。 (1) Aさんが玉を1個取り出し,取り出した玉を袋の中に戻さずに,続けてBさんが玉を1個取り出す。2人の玉の取り出し方は全部で何通りか。 【解】5×4＝20通り (2) Aさんが玉を1個取り出し,取り出した玉を袋の中に戻した後,Bさんが玉を1個取り出す。2人が取り出した玉に書かれた数字の和が7以下となる確率を求めなさい。 【解】取り出し方は全部で,52＝25通り (和が7以下の確率)＝1−(和が7より大の確率) 　(3,5) (4,4) (4,5) (5,3) (5,4) (5,5) の6通りで, 　　　確率＝1−＝
４	桐光学園高校　（Ｒ６年）　★★★	８	三重県立高校　（Ｒ６年）　★★
袋の中に,赤玉4個,白玉3個,黒玉1個の8個の玉が入っている。 (1) 3人とも赤玉を取り出す確率 【解】赤→赤→赤 確率＝ 4 × 3 × 2 ＝ 1 8 7 6 14 (2) Bが2個目の白玉を取り出す確率 【解】白→白 確率＝ 3 × 2 ＝ 3 8 7 28 (3) 袋の中に3色すべての色の玉が残っている確率 【解】 8個から3個の取り方は,8C3＝ 8×7×6 ＝56通り 3×2×1 (3色が残る確率)＝(黒を取らない確率) ・赤だけ3…4C3＝4C1＝4通り ・赤2白1…4C2×3C1＝6×3＝18通り ・赤1白2…4C1×3C2＝4×3＝12通り 確率＝(4＋18＋12)÷56=34/56＝17/28		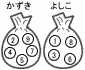かずきさんの袋に2,4,5,7,9の数が書かれた玉を,よしこさんの袋に1,3,6,8,の数が書かれた玉を入れたとき,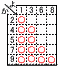 (1) このゲームで,かずきさんが勝つ確率を求めなさい。 【解】右表(〇)より,確率＝12÷20＝ (2) かずきさんの袋の2,4,5,7,9の数が書かれたいずれか１個の玉を取り出し,その玉をよしこさんの袋に入れ,ゲームをしたところ,かずきさんが勝つ確率と,よしこさんが勝つ確率が等しくなった。このとき,かずきさんの袋の2,4,5,7,9のいずれの玉を,よしこさんの袋に入れたか,その玉に書かれた数を答えなさい。 【解】なるべく大きい数を移して,2通り増やす ・9を移すと,4通り増えて不適 ・7を移すと,2通り増えて,勝率が共にで等しくなる

［TOP］　［問題に戻る］　　★　中　　★★　やや難　　★★★　難