| 俁俀丂揾傝暘偗丂乮棯夝乯 |
| 俁俀丂揾傝暘偗丂乮棯夝乯 |
| 侾 | 恄撧愳導棫崅峑/摿怓丂乮俼俆擭乯丂仛仛仛 | 俆 | 戝嶃惎岝妛堾崅峑丂乮俼係擭乯丂仛仛仛 |
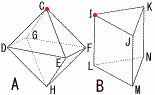 (1) 2偮傪慖傫偱愒偔拝怓偟報傪偮偗傞偲偒, (1) 2偮傪慖傫偱愒偔拝怓偟報傪偮偗傞偲偒,亂夝亃 A乧C偲懠偺1揰傪慖傇偲偒, 丒C偲(D,E,F,G)偼夞揮摨埵抲偱,1捠傝 丒C偲H偱1捠傝 丂傛偭偰,A偼1亄1亖2捠傝 B乧I偲懠偺1揰傪慖傇偲偒, 丒I偲(J,K)偼夞揮摨埵抲偱,1捠傝 丒I偲L偱1捠傝 丒I偲(M,N)偱2捠傝 丂傛偭偰,B偼1亄1亄2亖4捠傝 (2) 3偮傪慖傫偱愒偔拝怓偟報傪偮偗傞偲偒, 亂夝亃 A乧C偲懠偺1揰傪慖傇偲偒, 丒C偲(DE,EF,FG,GD)偼夞揮摨埵抲偱,1捠傝 丒C偲(DF,EG,DH,EH,FH,GH)偼夞揮摨埵抲偱,1捠傝 丂傛偭偰,A偼1亄1亖2捠傝 B乧I偲懠偺1揰傪慖傇偲偒, 丒I偲JK偱1捠傝 丒忋柺偐傜2揰,壓柺偐傜1揰偼夞揮摨埵抲偱,1捠傝 偲(JL,JM)偱2捠傝 丂傛偭偰,B偼1亄1亄2亖4捠傝 |
丂奺椞堟傪愒,惵,墿偺3怓巊偭偰揾傝暘偗傞丅偨偩偟,3怓偡傋偰偺怓傪巊偆傕偺偲偟,椬傝崌偆椞堟偵偼摨偠怓傪揾傜側偄傛偆偵偡傞丅 (1) 恾1偺1乣4偺椞忛傪揾傝暘偗傞曽朄偼[丂丂]捠傝偁傞丅 亂夝亃3怓偱3偐強(2僷僞乕儞) 丂(3亊2亊1)亊2亖(3亊2亊1)亊5亖30捠傝 亂夝亃揾傝暘偗曽偼塃恾 丂偙傟偑夞揮偟偰,a偼1乣5偺5僷僞乕儞 丂(3亊2亊1)亊5亖30捠傝 亂夝亃揾傝暘偗曽偼塃恾 傾 夞揮偟偰3僷僞乕儞 僀 夞揮偟偰1僷僞乕儞 僂 夞揮偟偰6僷僞乕儞 傾乣僂傛傝,(3亊2亊1)亊10亖60捠傝 |
||
| 俀 | 摨巙幮崅峑丂乮俼係擭乯丂仛仛仛 | 俇 | 宑滀媊弇巙栘崅峑丂乮俼係擭乯丂仛仛仛 |
亂夝亃 (1) 傾乣僂傪3怓偱  3怓偱3偐強傪揾傞偐傜,3亊2亊1亖6捠傝 3怓偱3偐強傪揾傞偐傜,3亊2亊1亖6捠傝(2) 惵偺5僷僞乕儞嘆乣嘍,巆傝傪2怓偱 嘆 2捠傝丂丂嘇 4捠傝 嘊 4捠傝丂丂嘋 4捠傝 嘍 2怓偱3偐強傪揾傞偐傜6捠傝 丂2亄4亊3亄6亖20捠傝 |
丂棫曽懱偺6柺傪偸傝暘偗傞偲偒 (1) 忋柺傪愒偲偟,巆傝傪5怓偱 掙柺偼,愒埲奜偺5捠傝 懁柺偼夞揮偱擇廳偵側偭偰偄傞偐傜, 丂5亊(4亊3亊2亊1亐4)亖30捠傝 忋丒掙柺(5捠傝)仺懁柺(6捠傝) 忋壓斀揮偱擇廳偵側偭偰偄傞偐傜, 丂5亊6亐2亖15捠傝 (3) 偳傟偐2柺偼摨怓 傾 2柺偑椬傝崌傢側偄偲偒,(2)傛傝15捠傝 僀 2柺偑椬傝崌偆偲偒,巆傝傪4怓偱 丂忋壓斀揮偱擇廳偵側偭偰偄傞偐傜, 丂丂5亊(4亊3亊2亊1)亐2亖60 傾僀傛傝,15亄60亖75捠傝 |
||
| 俁 | 拀攇戝晬懏嶁屗崅峑丂乮俼係擭乯丂仛 | ||
 丂拞墰偵敀偑偔傞妋棪傪媮傔側偝偄丅 丂拞墰偵敀偑偔傞妋棪傪媮傔側偝偄丅亂夝亃 怓偺揾傝曽偼慡晹偱,4亊3亊2亖24捠傝 嵍塃偺怓偼,(R,B) (R,Y) (B,Y)偑奺2捠傝 丂妋棪亖(2亊3)亐24亖6亐24亖 |
|||
| 係 | 戧愳崅峑丂乮俼俇擭乯丂仛仛 | 傾丂RRB RBB BBY BYY YYR YRR偦傟偧傟3捠傝偱, 丂3亊6亖18捠傝 僀丂RBY RYB BRY BYR YRB YBR 偺6捠傝 僂丂3亊3亊3亖27捠傝 |
|
| 丂壴巕偝傫偲懢榊偝傫偼恾偺恾埬偵偍偄偰,壴傃傜1枃偢偮偵怓墧昅偱怓傪揾傞偙偲偵偟偨丅 亂夝亃愒R,惵B,墿Y偲偟偰,丂丂丂丂丂乮仺塃傊偮偯偔乯 |
|||