| 夏休み きょうの１題 (８１９) 解 答 |  |
||||||
| 文字サイズを小にすると，Ａ４用紙に印刷できます | 月 日 （ ） | ||||||
| 愛光高校 （ R １年 【２】 ） ★★ | |||||||
車で50km離れた2地点の間を往復した。行きは20分間渋滞に巻き込まれ，ガソリンを3.66L消費した。帰りは70分間渋滞に巻き込まれ，ガソリンを4.06L消費した。この車は渋滞に巻き込まれていない時には1km進むのにxmLだけガソリンを消費した。また，渋滞に巻き込まれている時には毎分ymLだけガソリンを消費し，渋滞に巻き込まれている時の車の速さは毎分100mであった。このとき，x,yの値を求めよ。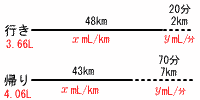 【解】xとyでは単位が違うから注意！行きの渋滞は，100m/分×20分＝2000m＝2km 渋滞なしは，50−2＝48km 帰りの渋滞は，100m/分×70分＝7000m＝7km 渋滞なしは，50−7＝43km
|
|||||||
 【類題】土浦日本大高校 （ R １年 【３】 ）2.8km離れた駅と学校がある。大輔君は徒歩で,駅から学校に分速80mで移動した。先生は自転車で,大輔君が出発するのと同時に学校を出発し,分速xmで駅に向かった。すると,出発してからy分後に花屋の前で2人はすれちがい,その4分後に先生は駅に到着した。  このとき,次の[ ]をうめなさい。(1) 大輔君が学校に到着するのは，駅を出発してから[ ]分後である。 【解】2800÷80＝ 35 分後 (2) 駅から花屋までの距離をxを用いて表すと[ ]xm，yを用いて表すと[ ]ymである。 【解】分速×分より， 先生は，x×4＝ 4x m 大輔君は，80×y＝ 80y m (3) x＝[ ]，y＝[ ]である。 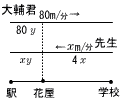 【解】(2)より，4x＝80yで，x＝20y …ア先生の道のりを考えると，xy＋4x＝2800 …イ アをイに代入して，20y2＋80y＝2800で，y2＋4y−140＝0 (y−10)(y＋14)＝0より，y＝10,−14 y＞0だから，y＝10 これをアに代入して，x＝20×10＝200 よって，x＝ 200，y＝ 10 |
|||||||
| 【類題】中央大杉並高校 （ R １年 【１】 ） メロスは村で用事を済ませ,城まで2400mのところまで戻ってきました。日没まではあと13分あります。今から城に向かって途中１回も休まずに日没ちょうどに城へ到着するためには,何分歩いて何分走れば良いか答えなさい。ただし,メロスの歩く速さは80m/分,走る速さは250m/分とします。 【解】x分歩くとすると，(13−x)分走ることになるから， 80x＋250(13−x)＝2400で，x＝5 よって，5分歩き，8分走る |
|||||||
