| 1 |
四天王寺高校 (R5年) ★ |
6 |
大阪府立高校C (R5年) ★★ |
\(\sqrt{847n}\)が整数となる自然数nのうち,最も小さいものはn=( )です。このとき,\(\sqrt{847n}\)=( )です。
|
nを自然数とする。n≦\(\sqrt{x}\)≦n+1を満たす自然数xの個数が100であるときのnの値を求めなさい。
|
| 2 |
桃山学院高校 (R5年) ★ |
7 |
桐朋高校 (R5年) ★ |
\(\sqrt{\frac{2023}{n}}\)が自然数となるような自然数nをすべて求めなさい。
|
1+√3の整数部分をa,小数部分をbとするとき,ab+b2の値を求めよ。
|
| 3 |
京華高校 (R5年) ★★ |
8 |
桐蔭学園高校 (R4年) ★★★ |
\(\sqrt{\frac{20a}{3}}\)が2桁の自然数の中で最も大きくなるよ うな自然数aの値を求めよ。
|
ある数の整数部分を考える。たとえば,4の整数部分は4,√2の整数部分は1である。このとき,次の[ ]に最も適する数字を答えよ。
(1) √10の整数部分は[ア] である。
\((2) \sqrt{n}\)の整数部分が3以上5以下となるnは全部で[イ][ウ]個である。ただし,nは正の整数である。
(3) 10から100までの正の整数を考える。それらの正の平方根の整数部分をすべて加えると[エ][オ][カ]である。
|
| 4 |
西大和学園高校(R4年) ★★★ |
\(\sqrt{28(118-3n)}\)が整数となる自然数nの値をすべてを求めよ。
|
| 5 |
中央大杉並高校(R6年) ★★★ |
9 |
明治大付属中野高校(R6年) ★★★ |
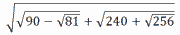 |
を計算しなさい。 |
|
5−√7の整数部分をa,小数部分をbとするとき,
| 3a2−5ab+2b2 |
の値を求めなさい。 |
| a2−ab |
|