 関数 |
５ 一次関数３ | 月 日（ ） |
| 関数 |
５ 一次関数３ | 月 日（ ） |
| １ | 群馬県立高校 （Ｒ４年） ★ | ６ | 京都成章高校 （Ｒ４年） ★★ |
| 直線y＝3x＋5に平行で,点(2,4)を通る直線の式を求めなさい。 |
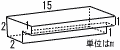 図のような2つの直方体を連結した形の水タンクが水平な台に置かれている。水が入っていない状態の水タンクに毎秒2m3ずつ水を入れるとき,水を入れはじめてからx秒後の水の深さをymとする。ただし,直方体を連結した部分に壁はなく,底面や側面の厚さは考えなくてよいものとする。(1) 水タンクの体積を求めなさい。 (2) x＝15のときのyの値を求めなさい。 (3) x＝30のときのyの値を求めなさい。 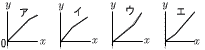 (4) 次のアからエまでのグラフのうち,xとyの関係を最もよく表しているグラフを1つ選び,記号で答えなさい。(5) 毎秒2m3ずつ水を入れたとき水タンクが満水になる時間から,ちょうど10秒だけ短い時間で満水にするためには,毎秒何m3ずつ水を入れればよいか求めなさい。 |
||
| ２ | 大阪府立高校Ｃ高校 （Ｒ４年） ★ | ||
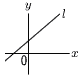 a,bを0でない定数とする。右図において,ℓは二元一次方程式ax＋by＝1のグラフを表す。次のア～エのうち,a,bについて述べた文として正しいものを一つ選び,記号を○で囲みなさい。ア aは正の数であり,bも正の数である。 イ aは正の数であり,bは負の数である。 ウ aは負の数であり,bは正の数である。 エ aは負の数であり,bも負の数である。 |
|||
| ３ | 市立福山高校 （Ｒ５年） ★★ | ||
| ３つの直線y＝x－7,y＝－2x＋8,y＝axがあります。a＝2のとき,この3つの直線は交わり三角形ができます。この3つの直線で三角形ができないようなaの値は全部で何個あるか,その個数を求めなさい。 |
|||
| ４ | 土浦日大高校 （Ｒ６年） ★★ | ||
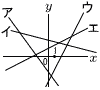 1次関数y＝ax＋bについて,(1) a＞0,b＜0のとき図のア～エのうち,この関数のグラフとして適切なものは[ ]である。 (2) a＋b＞0,ab＜0のとき,図のア～エのうち,この関数のグラフとして適切なものは[ ]である。 |
|||
| ５ | 広島県立高校 （Ｒ５年） ★★ | ７ | 國學院大久我山高校 （Ｒ５年） ★ |
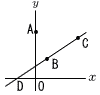 図のように,y軸上に点A (0,8))があり,関数y＝ x＋2のグラフ上にx＞0の範囲で動く2点B,Cがあります。点Cのx座標は点Bのx座標の4倍です。また,このグラフとx軸との交点をDとします。(1) 線分ACがx軸に平行となるとき,線分ACの長さを求めなさい。 (2) DB＝BCとなるとき,直線ACの傾きを求めなさい。 |
(1) 異なる2点(p,p2),(q,q2)を通る直線の傾きをp,qを用いて表しなさい。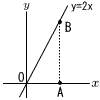 (2) 図のように,直線y＝2x, 2点A(1,0),B(1,b)がある。Oは原点,点Ｂは直線y＝2x上の点である。① bの値を求めなさい。 ② OBの長さを求めなさい。 |
||
