 関数 |
４ 一次関数２ | 月 日（ ） |
| 関数 |
４ 一次関数２ | 月 日（ ） |
| １ | 安田女子高校 （Ｒ４年） ★ | ５ | 奈良大附属高校 （Ｒ４年） ★★ |
| グラフの傾きが－5で,点(－2,0)を通る１次関数の式を求めなさい。 |
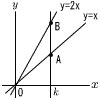 図のように.2つの直線y＝xとy＝2xがあり,直線x＝k(k＞0) との交点をそれぞれA,Bとする。(1) 線分ABの長さが4のとき,kの値を求めなさい。 (2) △OABの面積が32のとき,kの値を求めなさい。 (3) y＝kとy＝2xの交点をCとする。△OACの面積が27のとき,kの値を求めなさい。 |
||
| ２ | 帝塚山学院泉ヶ丘高校 （Ｒ４年） ★★ | ||
| 3直線 2x－y－3＝0,x＋y－6＝0,ax－y＋4＝0によって三角形が作られない場合の定数aの値をすべて求めなさい。 |
|||
| ３ | 東京学芸大附属高校 （Ｒ６年） ★ | ||
| アメリカなどの国では日本とは異なる単位が使われることがある。時速40kmで進む自動車Ａがｘ時間進んだときの道のりをykmとして,yをxの式で表すとy＝40xである。 自動車Ａと同じ速さで進む自動車Bがx時間進んだときの道のりをzマイルとして,zをxの式で表しなさい。ただし,1マイルは1.6kmであるとする。 |
|||
| ４ | 千葉県立高校 （Ｒ５年） ★★ | ６ | 東北高校 （Ｒ５年） ★★ |
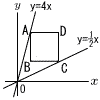 図のように,直線y＝4x上の点Aと直線y＝ x上の点Cを頂点にもつ正方形ABCDがある。点Aと点Cのx座標は正で,辺ABがy軸と平行である。(1) 点Aのy座標が8であるとき. ① 点Aのx座標を求めなさい。 ② 2点A,Cを通る直線の式を求めなさい。 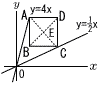 (2) 正方形ABCDの対角線ACと対角線BDの交点をEとする。点Eのx座標が13であるとき,点Dの座標を求めなさい。 |
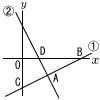 図で,直線①は関数y＝x－7のグラフ,直線②は関数y＝axのグラフです。直線①と直線②の交点をA.,直線①とx軸との交点をB,y軸との交点をCとします。また,直線②とx軸との交点をDとすると,そのx座標は4です。(1) aの値を求めなきい。 (2) 点Aの座標を求めなさい。 (3) △ACDの面積を求めなさい。 (4) x軸上に,x座標が点Bのx座標より大きい点Pをとります。△ACPの面積が△ACDの面積の になるとき,点Pのx座標を求めなさい。 |
||
