| 32 ダイヤグラム | 月 日( ) |
| 32 ダイヤグラム | 月 日( ) |
| 1 | 岐阜県立高校 (R5年) ★ | 3 | 茨城県立高校 (R4年) ★★★ | ||||||||||||
モノレールが13時にA駅を出発してからx分後の,B駅からモノレールのいる地点までの道のりをymとする。13時から13時56分までのxとyの関係をグラフに表すと,図のようになる。(ただし,モノレールや駅の大きさは考えないものと 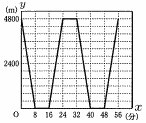 する) する)(1) モノレールがA駅とB駅の問を走行するときの速さは,分速何mであるかを求めなさい。 (2) xの変域を次の(ア),(イ)とするとき,yをxの式で表しなさい。 (ア) 0≦x≦8のとき (イ) 16≦x≦24のとき (3) 花子さんは13時にB駅を出発し,モノレールの線路沿いにある歩道をA駅に向かって一定の速さで歩いた。花子さんはB駅を出発してから56分後に,モノレールと同時にA駅に到着した。 (ア) 花子さんが初めてモノレールとすれ違ったのは,モノレールが13時にA駅を出発してから,何分後であったかを求めなさい。 (イ) 花子さんは,初めてモノレールとすれ違った後,A駅に向かう途中で,B駅から戻ってくるモノレールに迫い越された。花子さんが初めてモノレールとすれ違ってから途中で追い越されるまでに,歩いた道のりは何mであったかを求めなさい。 |
S町では,2700m離れた2地点A,B間で,2台の無人自動運転バスP,Qの導入実験を行った。下の表は,バスP,Qの走行の規則についてまとめたものである。また,下の図は,地点Aを出発してからx分後の地点Aからの距離をymとして,xとyの関係をグラフに表したものである。 ただし,2地点A,Bを結ぶ道路は直線とする。
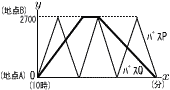 (1) (1)① バスPが2回日に地点Bに到着した時刻を求めなさい。 ②バスQの,地点Bに到着するまでの速さは分速何mか求めなさい。 (2) 2地点A,Bを結ぶ道路上に地点Cがある。地点Cを,地点Aに向かうバスQが通過した8分後に,地点Aに向かうバスP が通過した。地点Cは地点Bから何mのところにあるか求めなさい。 |
||||||||||||||
| 2 | 高知県立高校 (R6年) ★ | (1) 13時に遊園地を出発して駅に向かうバスについて,yをxの式で表しなさい。ただし,xの変域は書かなくてよい。 (2) 13時15分に駅を出発したバスは,13時20分に遊園地を出発したバスと,13時何分に駅から何kmの地点ですれ違うかを求めなさい。 |
|||||||||||||
駅から高台にある遊園地までの道のりは6kmあり,駅と遊園地の間をバスが連行している。次の図は,13時からx分後の,駅からバスまでの道のりをykmとして,13時から14時までの,駅を出発して遊園地に向かうバスと,遊園地を出発して駅に向かうバスの,xとyの関係を表したグラフである。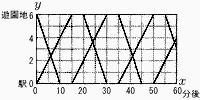 (右へつづく→) (右へつづく→) |
|||||||||||||||