 図形 |
１ 合同な図形 | 月 日（ ） |
| 図形 |
１ 合同な図形 | 月 日（ ） |
| １ | 岩手県立高校 （Ｒ４年） ★ | ５ | 福島県立高校 （Ｒ４年） ★ |
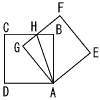 2つの合同な正方形ABCDとAEFGがあり,それぞれの頂点のうち頂点Aだけを共有しています。辺BCと辺FGは1点で交わっていて,その点をHとします。このとき,BH＝GHであることを証明しなさい。 |
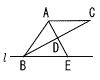 △ABCがあり,直線l は点Bを通り辺ACに平行な直線である。また,∠BACの二等分線と辺BC, lとの交点をそれぞれD,Eとする。 AC＝BEであるとき,△ABD≡△ACDとなることを証明しなさい。 |
||
| ２ | 新潟県立高校 （Ｒ５年） ★ | ６ | 埼玉県立高校 （Ｒ５年） ★★ |
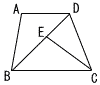 図のように,AC//BCの台形ABCDがあり,∠BCD＝∠BDCである。対角線BD上に,∠DBA＝∠BCEとなる点Eをとるとき,AB＝ECであることを証明しなさい。 |
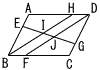 下の図のように,平行四辺形ABCDの辺AB,BC,CD,DA上に4点E,F,G,Hをそれぞれとり,線分EGとBH,DFとの交点をそれぞれI,Jとします。AE＝BF＝CG＝DHのとき,△BEI≡△DGJであることを証明しなさい。 |
||
| ３ | 大阪教育大平野校舎高校 （Ｒ６年） ★★ | ７ | 高知県立高校 （Ｒ６年） ★ |
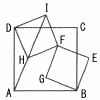 右の図において,四角形ＡBDＤ,BEFG,DHFI はすべて正方形である。それぞれの正方形は,図のように2点を他の正方形と共有している。3点Ａ,H,Ｉが同一直線上にあるとき,(1) AD＝AFを証明しなさい。 (2) 3点A,G,Eが同一線上にあることを示しなさい。 |
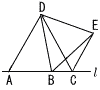 右の図のように,直線l上に3点A,B,Cをとり,辺ACを一辺とする正三角形ACDと,辺DBを一辺とする正三角形BEDをつくり,点Cと点Eを結ぶ。(1) △ABD≡△CEDを証明しなさい。 (2) AD＝4cmのとき,四角形BCEDの面積を求めなさい。 |
||
| ４ | 広島県立高校 （Ｒ６年） ★ | ８ | 西大和学園高校 （Ｒ６年） ★★ |
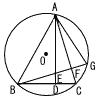 右の図のように,△ABCは鋭角三角形で,頂点A,B,Cは円Oの円周上にあります。点Aから辺BCに垂線ADを引きます。また,点Bから辺ACに垂線を引き,線分ADとの文点をE,辺ACとの交点をF,円０との交点をGとします。さらに,点Aと点Gを結ぴます。このとき,△AEF≡△AGFであることを証明しなさい。 |
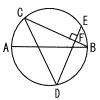 図のように,ABを直径とする円周上に2点C,Dがあり,円周上に点EをBCとDEが垂直になるようにとる。BCとDEの交点を Fとする。このとき,三角形CAEと三角形ACDが合同であることを証明せよ。 |
||
印刷用