 図形 |
１２ 二等辺三角形 | 月 日（ ） |
| 図形 |
１２ 二等辺三角形 | 月 日（ ） |
| １ | 盈進学園高校 （Ｒ５年） ★★ | ４ | 灘 高校 （Ｒ５年） ★★ |
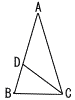 次のようなAB＝AC,BC＝AD＝CD,BC＝1cmの図形があります。(1) ∠ADCの大きさを求めなさい。 (2) BDの長さを求めなさい。 (3) ACの長さを求めなさい。 |
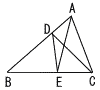 右の図において,BD＝DC＝CA,BE＝EAである。∠DEAの大きさが32度のとき,∠ABCの大きさは( )度である。 |
||
| ２ | ラ・サール高校 （Ｒ４年） ★★★ | ５ | 早大高等学院 （Ｒ４年） ★★★ |
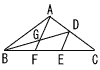 △ABCはAB＝AC＝1,∠BAC＝120°の二等辺三角形である。∠ABCの二等分線と辺ACの交点をDとし,CD＝CEとなる点Eを辺BC上にとる。次に,BC上にDE//AFとなる点Fをとり,AFとBDの交点をGとする。このとき,EFの長さと△AGDの面積を求めよ。 |
AB＝AC,BC＝1,∠ABC＝72°の二等辺三角形ABCについて, (1) ∠ABCの二等分線と辺ACとの交点をDとするとき,線分 CDの長さを求めよ。 (2) 頂点Bから辺ACへ垂線をひき,辺ACとの交点をEとするとき,BE2の値を求めよ。 |
||
| ３ | 盈進高校 （Ｒ６年） ★ | (2) 辺CFの長さを求めなさい。 (3) △CFGの面積がxcm2であるとき,△CDEの面積をxを用いて表しなさい。 |
|
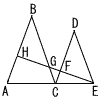 △ABCは,AB＝CB＝6cmの二等辺三角形,△CDEは,CD＝ED＝4cmの二等辺三角形であり,この2つの三角形は相似である。また,A,C,EとE,F,G,Hは,それぞれ同一直線上にあるものとする。CG＝1cmのとき,(1) △CFGと△DFEの面積比を求めなさい。 (右へつづく→) |
|||
