データの活用	２５　コイン (確率)	月　　　日（　　）
以下の問題では,どのコインも表と裏の出方は同様に確からしいものとします。

１	明大付属八王子高校　（Ｒ５年）　★★	５	都立日比谷高校　（Ｒ４年）　★
100円硬貨と50円硬貨が2枚ずつあります。この4枚の硬貨を同時に投げるとき,表が出た硬貨の合計金額が100円以上200円以下となる確率を求めなさい。		1枚の硬貨を投げるとき,表が出たら得点1,裏が出たら得点2とする。 　この硬貨を3回投げ,1回目の得点をa,2回目の得点をb,3回目の得点をcとするとき,b＝ac となる確率を求めよ。
２	日本大第二高校　（Ｒ６年）　★★★	６	興南高校　（Ｒ４年）　★
1枚の硬貨を3回投げる。それぞれの出方に対して表が出れば1点,裏が出れば2点を与えるものとする。得点の合計が5点となる確率を求めよ。		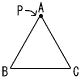図のような正三角形ABCの頂点Aに点Pがある。1枚の硬貨を投げて,表が出ると点Pは時計回りにとなりの頂点へ動き,裏が出ると点Pは反時計回りにとなりの頂点へ動く。硬貨を3回投げたとき,点Pが頂点Aにある確率を求めなさい。
３	慶應義塾志木高校　（Ｒ５年）　★★★	７	三重高校　（Ｒ４年）　★★
1枚のコインを6回投げるとき,次の確率を求めよ。 (1) 表が1回以上出る確率 (2) 表が連続して3回以上出る確率		500円,50円,10円の硬貨が1枚ずつ,100円の硬貨が2枚ある。この5枚を同時に投げる。 (1) 5枚のうち,少なくとも1枚は表となる確率は[　　] である。 (2) 表となった硬貨の合計金額が,600円以上になる確率は[　　] である。
４	桐光学園高校　（Ｒ６年）　★★★	(2) コインを3回投げるとき,PとQが同じ頂点にある確率を求めよ。 (3) コインを6回投げるとき,PとQが少なくとも1回は同じ頂点にある確率を求めよ。
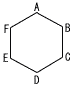一辺が1cmの正六角形ABCDEFの辺上を2点P,Qが時計回りに動く。はじめ,点Pは点Aにあり,点Qは点Dにある。点Pはコインを投げるごとに表が出れば1cm,裏が出れば2cmずつ動く。点Qはコインを投げるごとにコインの表裏に関わらず3cmずつ動く。 (1) コインを2回投げるとき,PとQが同じ頂点にある確率を求めよ。 　　　　　　　　　　　　　　　(右へつづく→)

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用