 データの活用 |
２７ その他 (確率) | 月 日（ ） |
| 以下の問題では,どの事柄が起こることも同様に確からしいものとします。 | ||
| データの活用 |
２７ その他 (確率) | 月 日（ ） |
| 以下の問題では,どの事柄が起こることも同様に確からしいものとします。 | ||
| １ | 沖縄県立高校 （Ｒ６年） ★★★ | ４ | 西大和高校 （Ｒ４年） ★★★ | ||
| A,B,C,Dの4人がプレゼントをーつずつ持ちより,交換会を開く。プレゼントはすべて異なるものとし,A,B,C,Dの4人が用意したプレゼントをそれぞれa,b,c,dとする。交換の方法は,外見が|司じギフト箱を4人分用意し,各箱にプレゼントをーつずつ入れたうえで,よく混ぜて4人に箱を一つずつ配り,4人は配られた箱の中のプレゼントを受け取る。交換の結果によっては自分が用意したプレゼントを受け取ることもある。 (1) プレゼントの受け取り方は全部で何通りあるか答えなさい。 (2) Aさんがaではないプレゼントを受け取る確率を求めなさい。 (3) A,B,C,Dの4人全員が,自分で用意したプレゼントを受け取らない確率を求めなさい。 |
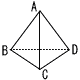 正四面体ABCDがあり,この正四面体の頂点を点Pが1秒ごとに次の規則に従って移動する。
|
||||
| ５ | 早稲田佐賀高校 （Ｒ６年） ★★ | ||||
| A,B,C,Dと書かれた4つのボールを無作為に横1列に並べるとき,AのボールがBのボールよりも右にくる確率を求めよ。 |
|||||
| ２ | 愛光高校 （Ｒ５年） ★★★ | ６ | 立教新座高校 （Ｒ５年） ★★★ | ||
A,B,Cの3つの袋があり,Aの中には1から6,Bの中には1から10,Cの中には1から4の数字が書かれたカードがそれぞれ1枚ずつ入っている。A,B,Cの袋から1枚ずつカードを取り出し,そのカードの数字をそれぞれa,b,cとし,直線y＝ x＋cをl とするとき,(1) l が直線y＝2xと平行になる確率を求めよ。 (2) l が点(6,10)を通る確率を求めよ。 |
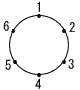 図のように,円周を6等分した点にそれぞれ1から6までの数字がついています。さいころを3回投げて,出た目と同じ数字の点を結んでできる図形を考えます。すべて異なる目が出た場合は三角形となり,同じ目が2回出た場合は線分となり,同じ目が3回出た場合は点となります。このとき,次の確率を求めなさい。(1) 三角形にならない確率 (2) 直角三角形になる確率 |
||||
| ３ | 茨城県立高校 （Ｒ６年） ★★★ | ７ | 早大高等学院 （Ｒ６年） ★★★ | ||
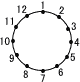 1から6までの数が１つずつ書かれた6枚の赤色のカード1⃣,2⃣…6⃣と,7から12までの数が1つずつ書かれた6枚の青色のカード7⃣,8⃣… がある。赤色のカードをよくきってから1枚引き,そのカードに書かれた数をaとする。同様に,青色のカードをよくきってから1枚引き,そのカードに書かれた数をbとする。(1) a＋bが3の倍数となる確率として正しいものを,次のア～オの中から1つ選んで,その記号を書きなさい。 ア  イ  ウ  エ  オ  (2) 図のように円周を12等分する点があり,時計回りにそれぞれ１から12までの番号をつけ,a,bと同じ番号の点にそれぞれコマを置く。例えば,a＝3,b＝７のとき,円周上の番号3,番号7の2つの点にそれぞれコマを置く。 ① コマを置いた2つの点が,この円の直径の両端となる確率を求めなさい。 ② 番号1の点とコマを置いた2つの点が,直角三角形の3つの頂点となる確率を求めなさい。 |
図のような1辺の長さが1の立方体の辺上を2点A, Bが次のルールでそれぞれ移動する。
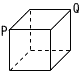 (1) 2点A,Bがともに頂点Pから出発して,その1秒後にAB＝√2となる確率を求めよ。(2) 2点A,Bがそれぞれ頂点P,Qから出発して,その1秒後もAB＝√2となる確率を求めよ。 (3) 2点A,Bがともに頂点Pから出発して,その2秒後にAB＝√3となる確率を求めよ。 (4) 2点A,Bがともに頂点Pから出発して,その3秒後にAB＝√2となる確率を求めよ。 |
||||
