 関数 |
３ 一次関数１ | 月 日（ ） |
| 関数 |
３ 一次関数１ | 月 日（ ） |
| １ | 筑波大附属坂戸高校 （Ｒ４年） ★ | ５ | 桜美林高校 （Ｒ５年） ★ | ||||||||||||||||
| 2点(6,11),(1,－4)を通る直線の式を求めなさい。 |
座標平面上に点A(－2,10), B(4,－6), C(－5,k) がある。この点が 一直線上にあるとき,kの値を求めなさい。 |
||||||||||||||||||
| ２ | 聖愛高校 （Ｒ４年） ★★ | ６ | 京華高校 （Ｒ４年） ★★ | ||||||||||||||||
(1) yがxに反比例するとき,表の[ ]にあてはまる値を求めなさい。 (2) yがxの1次閔数であるとき,表の[ ]にあてはまる値を求めなさい。 |
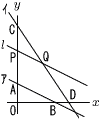 図のような,直線y＝− x＋3…アがある。アとy軸,x軸との交点をそれぞれA,Bとし,2点C(0,12),D(8,0)を通る直線をイとする。また,直線アと平行で,線分AC上の点Pを通る直線をl とする。イとl の交点をQとするとき, (1) 直線イの式を求めよ。 (2) 点Pの座標が(0,8)であるとき,△QABの面積を求めよ。 (3) △QABの面積が四角形ABDCの面積の 倍になるとき, 直線l の式を求めよ。 |
||||||||||||||||||
| ３ | 明治学院高校 （Ｒ５年） ★★ | ７ | 大阪教育大附属平野校舎 （Ｒ５年） ★★ | ||||||||||||||||
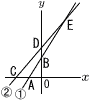 図のように,2直線y＝ x＋s…①,y＝ x＋t…②（0＜s＜t）がある。①とx軸,y軸との交点をそれぞれA,B,②と,x軸,y軸との交点をそれぞれC,D,①と②の交点をEとする。(1) △AOBの面積をsを用いて表せ。 (2) 点Eのx座標を.s,tを用いて表せ。 (3) s＝3で,△AECと△ODCの面積が等しいとき,tの値を求めよ。 |
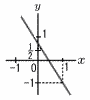 y＝ax＋bのグラフが右の図のようになっているとき，次の等式,不等式を満たす整数k,l,m,nの値を求めなさい。(1) k＜b＜k＋1 (2) l＜a＜l＋1 (3) a＋b＝m (4) n＜－a＋b＜n＋1 |
||||||||||||||||||
| ４ | 愛媛県立高校 （Ｒ６年） ★ | ８ | 西大和学園高校 （Ｒ６年） ★★★ | ||||||||||||||||
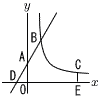 図は,1辺に4個の碁石を並べた正五角形で,並べた碁石は全部で15個である。1辺にn個の碁石を並べた正五角形をつくったとき,並ぺた碁石は全部で何個か,nを使って表せ。ただし,nは2以上の自然数とする。 |
直線4x＋5y＝2, ax＋3y＝0 の交点をPとし,直線－x＋2y＝7, 5x＋by＝－1 の交点をQとすると,P,Qは原点に関して対称になった。このとき,a,bの値を求めよ。 |
||||||||||||||||||
