| �@�X�@�� | �@�@�@���@�@�@���i�@�@�j |
| �@�X�@�� | �@�@�@���@�@�@���i�@�@�j |
| �P | �Q�n�������Z�@�i�q�S�N�j�@�� | �S | �L���������Z�@�i�q�U�N�j�@�� | ||
| �@x��y�̊W��y��ax2�ŕ\����,x���|2�̂Ƃ�,y��8�ł���Bx��3�̂Ƃ���y�̒l�����߂Ȃ����B �@ |
�@y��x��2��ɔ�Ⴕ,x��6�̂Ƃ�y��12�ł��B���̂Ƃ�,y��x�̎��ŕ\���Ȃ����B �@ |
||||
| �Q | ���s�{�����Z�@�i�q�U�N�j�@���� | �T | �}�g�啍����ˍ��Z�@�i�q�S�N�j�@�� | ||
| �@y��x��2��ɔ�Ⴕ,x��3�̂Ƃ�y���|54�ł���B���̂Ƃ�,y��x�̎��ŕ\���B �@ |
�@�{�[���𗎂Ƃ��ė����n�߂Ă���x�b���ɗ����鋗����y���Ƃ����,x��y�̊Ԃɂ�,���悻y��5x2�̊W������܂��45m�̍�������{�[���𗎂Ƃ��Ƃ��n�ʂɗ�����܂ʼn��b�����邩���߂Ȃ����B �@ |
||||
| �R | ��C�啍�����Z�@�i�q�U�N�j�@������ | �U | ���Q�������Z�@�i�q�U�N�j�@�� | ||
| �@�Ԃ̉^�]�ɂ�����,�^�]�肪�댯�������Ă���u���[�L������,���ۂɎԂ���~����܂ł̋������~�����Ƃ����B��~�����͎���2�̋����̘a�ł���B �@���� �@�^�]�肪�댯�������Ă���u���[�L�������n�߂�܂łɎԂ��i�ދ����̂��Ƃ�,�Ԃ̑����ɔ�Ⴗ��B �@(��) ����20km�ő��s�����Ƃ��̋�����6m�̏ꍇ,2�{�̑���(����40km)�ő��s�����Ƃ��̑��s������6�~2��12���12m�ƂȂ�B �A�������� �@�u���[�L�������n�߂Ă�����ۂɎԂ���~����܂łɐi�ދ����̂��Ƃ�,�Ԃ̑�����2��ɔ�Ⴗ��B[2��ɔ�Ⴗ��]�Ƃ͑�����2�{���Ȃ�Ɛ���������4�{��,������3�{�ɂȂ�Ɛ���������9�{�ɂȂ�Ƃ������Ƃł���B �@(��) ����20km�ő��s�����Ƃ��̐���������3m�̏ꍇ,2�{�̑���(����40km)�ő��s�����Ƃ��̐���������3�~22��3�~4��12���12m�ƂȂ�B �@����������,�@�A�̗�̏ꍇ,����20km�ő��s�����Ƃ��̒�~������6�{3��9���9m,����40km�ő��s�����Ƃ��̒�~������12�{12��24���24m�ƂȂ�B �@����20 m�ő��s�����Ƃ��̋�����6��,����������3���Ƃ���,���̊e�₢�ɓ����Ȃ����B�Ȃ�,�����������ƂȂ����ꍇ��,������P�ʂ��l�̌ܓ���,�����œ����Ȃ����B (1) �Ԃ�����50km�ő��s�����Ƃ��̏ꍇ�̒�~���������߂Ȃ����B (2) �Ԃ�����20km��x�{�̑����ő��s�����Ƃ��̒�~������x��p���ĕ\���Ȃ����B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�E�ւÂ���)�@ |
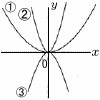 �@�}�ɂ�����,�������@,�A,�B�͂��ꂼ���y��ax2,y��bx2,y��cx2�̃O���t�ł���Ba,b,c��,�l�̏��������ɍ�������ׂď����B �@�}�ɂ�����,�������@,�A,�B�͂��ꂼ���y��ax2,y��bx2,y��cx2�̃O���t�ł���Ba,b,c��,�l�̏��������ɍ�������ׂď����B�@ |
||||
| �V | �c��`�m�u�؍��Z�@�i�q�U�N�j�@������ | ||||
�@�o�R�n�}�Ȃǂɏ�����Ă���R�[�X�̕��s���Ԃ��u�R�[�X�^�C���v�Ƃ����B�X�Η�s(s��0)�̎Ζʂ�o��Ƃ�,����dkm�̃R�[�X�^�C��T�́C�萔a,b,c��p����T��{(as�{bs�{c)�~d}���ƎZ�o�����Ƃ���B�X�Η�0�ŋ���2km�̃R�[�X�^�C����40��,�X�Η�0.1�ŋ���1km�̃R�[�X�^�C����26.5��,�X�Η�0.2�ŋ���1km�̃R�[�X�^�C����36���ƂȂ�B
(1�j�萔a,b,c�̒l�����߂�B (2) �X�Η�s�ŋ���9km�̃R�[�X�^�C����324���ł���Ƃ�,s�̒l�����߂�B |
|||||
| (3) ��~������72m�ƂȂ�Ƃ�,�Ԃ̑����͎�����k�������߂Ȃ����B |
|||||
�mTOP�n�mBACK�n�mNEXT�n�m���n�@�@���� �������� ��������@![]() ����p
����p