| 1 |
滋賀県立高校 (R4年) ★ |
5 |
近畿大付属高校 (R5年) ★ |
関数y=−3x2 について,xが−4から3まで増加したときの,yの変域を求めなさい。
|
a,bは定数とする。関数y=ax2について,xの変域が−2≦x≦bのとき,yの変域は2≦y≦8である。
このとき,a,bの値を求めよ。
|
| 2 |
都立日比谷高校 (R4年) ★★ |
6 |
中央大附属横浜高校 (R4年) ★★ |
一次関数y=ax+4において,xの変域が−3≦x≦6 のとき,yの変域は2≦y≦5である。定数aの値を求めよ。
|
−1≦x≦2のとき,2つの関数y=ax2とy=bx+a−3のyの変域が一致する。このとき,a,bの値を求めなさい。ただし,a<0,b>0とする。
|
| 3 |
桐光学園高校 (R6年) ★★ |
7 |
和光国府台女子高校 (R4年) ★★ |
関数y=x2について,xの変域が−2≦x≦pのとき,yの変域はq≦y≦p+12である。このとき,定数p,qの値を求めよ。
|
2つの関数y=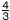 xとy=ax+bは,xの変域が0≦x≦6のときyの変域が等しく,この関数のグラフは1点で交わる。この交点を反比例y= xとy=ax+bは,xの変域が0≦x≦6のときyの変域が等しく,この関数のグラフは1点で交わる。この交点を反比例y=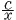 のグラフが通るとき,cの値を求めよ。 のグラフが通るとき,cの値を求めよ。
|
| 4 |
ラ・サール高校 (R6年) ★★ |
8 |
明治大付属中野高校 (R6年) ★★★ |
2つの関数y=−3x+aとy=x2があり,xの変域がb≦x≦4のとき,yの変域が一致するという。a,bの値の組をすべて求めよ。ただし,b<0とする。
|
関数y=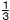 x2について,xの変域がa−6≦x≦aのとき,yの変域が0≦y≦9となります。このとき,aの値をすべて求めなさい。 x2について,xの変域がa−6≦x≦aのとき,yの変域が0≦y≦9となります。このとき,aの値をすべて求めなさい。
|