 関数 |
１６ 放物線と直線３ | 月 日（ ） |
| 関数 |
１６ 放物線と直線３ | 月 日（ ） |
| １ | ラ・サール高校 （Ｒ４年） ★★ | ４ | お茶の水女子大附属高校 （Ｒ４年） ★★ |
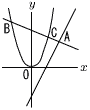 図のように2直線l ,mは点Aで垂直に交わり,l は放物線:y＝3x2と点B,Cで交わっている。直線l の方程式はy＝ax＋6,直線mの方程式はy＝2x＋b,点Aのx座標は5である。(1) 定数a,bの値 (2) 2点B,Cの座標 |
aを定数とし,a≠0とする。放物線①y＝ax2と直線②y＝a2x＋3aは2点A,Bで交わり,点Aのx座標は－1である。 (1) 交点A,Bの座標をそれぞれ求めなさい。 (2) 点Oを原点とするとき,△OABの面積と△OBCの面積が等しくなるような放物線①上の点Cの座標を求めなさい。ただし,点Cのx座標は,点Bのx座標より大きいものとする。 |
||
| ２ | 早稲田大高等学院 （Ｒ５年） ★★★ | ５ | 日本大第三高校 （Ｒ５年） ★★ |
| aを正の定数とする。放物線y＝x2と直線y＝ax＋2aとの交点を A,Bとし,放物線y＝x2と直線y＝(3√2－4)x＋6√2－8との交点をC,Dとする。ただし,点Aのx座標は－1であり,点Cのx座標は点Dのx座標よりも小さい。また,直線y＝ax＋2aとx軸との交点をEとする。 (1) aの値を求めよ。 (2) EA/EB の値を求めよ。 (3) 点Cのx座標を求めよ。 (4) 4点A,B,C,Dを頂点とする四角形の面積を求めよ。 |
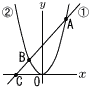 右の図のように,直線①のグラフと放物線②のグラフが2点A,Bで交わっている。さらに,①はx軸と点Cで交わっている。Ａ(4,8),C(－4,0),点Bのx座標を－2とする。ただし,座標の１目盛りを1cmとする。(1) 点Bの座標を求めなさい， (2) 点Bと原点Oについて対称な点をDとするとき,△ADBの面積を求めなさい。 (3) 点Bから直線ADに引いた垂線の長さを求めなさい。 |
||
| ３ | 愛光高校 （R６年） ★★★ | ６ | 中央大附属高校 （R６年） ★★★ |
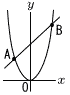 右の図のように放物線y＝x2と直線y＝x＋6があり,その交点をx座標が小さい順にＡ,Ｂとする。(1) 点Ａ,Ｂの座標を求めよ。答のみでよい。 (2) 直線y＝x＋6に関して点C(3,a)と対称な点Ｄが放物線上にあるとき,aの値と点Ｄの座標を求めよ。ただし,a≠9とする。 (3) 点Ｄを通り,四角形ＡＣＢＤの面積を２等分する直線の式を求めよ。 |
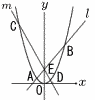 図のように,関数y＝x2のグラフと直線lの交点をＡ,Ｂ,関数y＝x2のグラフと直線mの交点をC,D,直線l,mの交点をE(0,2)とする。AE:EB＝1:3のとき,(1) 直線lの式を求めなさい。 (2)△ＡＥＣと△ＤＥＢの面積比が2:1のとき, (ア) 点Ｄのx座標を求めなさい。 (イ) 直線mの式を求めなさい。 |
||
