 関数 |
１９ 二つの放物線２ | 月 日（ ） |
| 関数 |
１９ 二つの放物線２ | 月 日（ ） |
| １ | 法政大高校 （Ｒ５年） ★★★ | ４ | 東大寺学園高校 （Ｒ５年） ★★ |
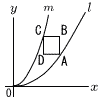 右の図の曲線l は放物線y＝ x2のx≧0の部分である。曲線mは放物線y＝ax2のx≧0の部分である。また,四角形ABCDは１辺3の正方形で,頂点Aは曲線l 上に,頂点Cは曲線m上にあり,辺ABはy軸に平行である。ただし,a＞とし,頂点Aのx座標は3よりも大きいものとする。(1) 頂点Aのx座標が4のとき,直線ACの式を求めなさい。 (2) a＝2のとき,頂点Aのx座標を求めなさい。 |
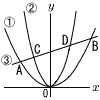 0＜a＜bとする。原点をOとするxy平面上に2つの放物線y＝a2x2…①,y＝b2x2…②と1つの直線y＝ax＋6…③があり,①と③が相異なる2点A,Bで交わり,②と③が相異なる2点C,Dで交わっている。ただし,Aのx座標はBのx座標より小さく,Cのx座標はDのx座標より小さいものとする。(1) A,Bの座標をそれぞれaを用いて表せ。 (2) 三角形OABの面積が30のとき,aの値を求めよ。 (3) (2)のとき,三角形OBDの面積が6であるとする。このとき,三角形OCAの面積を求めよ。 |
||
| ２ | 市立福山高校 （Ｒ４年） ★★ | ５ | 大阪産大附属高校 （Ｒ４年） ★★ |
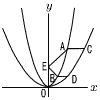 図のように関数y＝x2のグラフ上に2点A,Bがあり,関数y＝ x2のグラフ上に2点C,Dがあります。2点A,Cのy座標はどちらも8であり,2点B,Dのy座標はどちらも2です。また,y軸上を動く点Eがあります。ただし,点A,B,C,Dのx座標,点Eのy座標はいずれも正の数とします。(1) 点Cのx座標を求めなさい。 (2) △ACEと△EBDの面積が等しくなるとき,点Eの座標をすべて求めなさい。 (3) 線分CEと線分BEの長さの和CE＋BEが最小になるとき,点Eの座標を求めなさい。 |
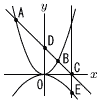 図のように,放物線y＝ x2上に2点A,Bがあり,点Aのx座標は－6,点Bのx座標は3である。直線ABとx軸,y軸との交点をそれぞれ点C,Dとする。点Cを通りy軸に平行な直線と放物線y＝ax2(a＜0)との交点をEとする。(1) 2点A,Bを通る直線の方程式を求めなさい。 (2) △OCAの面積を求めなさい。 (3) △EABの面積が18のとき,aの値を求めなさい。 |
||
| ３ | 日本大第二高校 （Ｒ６年） ★★★ | ６ | 明治大付属明治高校 （Ｒ６年） ★★★ |
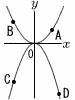 図のように放物線y＝ x2と放物線y＝－x2について,2点A,Bは放物線y＝x2上にあり,2点C,Dは放物線y＝－x2上にあるものとする。点A,Dのx座標は正であり,点B,Cのx座標は等しく,負である。また,点Ｂのy座標は点Ａのy座標より１大きく,点Ｄのy座標は点Cのy座標より１小さいものとする。(1) 点Ａのx座標が2のとき点Ｄの座標を求めよ。 (2) 点Ａのx座標をtとする。 BCの長さが50のとき,tの値を求めよ。 (3) 点Ａのx座標と点Dのx座標の差が2になるとき,点Ａの座標を求めよ。 |
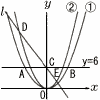 右の図のように2つの放物線y＝ x2…①,y＝ax2…②がある。放物線①と直線y＝6の2つの交点のうち,x座標が小さい方を点Ａ,もう1つの交点を点Ｂとする。また,点C(0,6)を通り,傾きが負である直線をl とし,放物線②と直線l の2つの交点のうち,x座標が小さい方を点D,もう1つの交点を点Eとする。△AOB＝△DOEであるとき。ただし,原点をOとし,a＞とする。(1) △AOBの面積を求めよ。 (2) CD:CE＝3:1のとき,aの値を求めよ。 (3) (2)のとき,△DPEの面積が,△DOEの面積の 倍となるように点Pを放物線①上にとる。このとき,点Pのx座標をすべて求めよ。 |
||
