 関数 |
２２ 放物線と円 | 月 日（ ） |
| 関数 |
２２ 放物線と円 | 月 日（ ） |
| １ | 洛南高校 （Ｒ５年） ★★★ | ４ | 桐光学園高校 （Ｒ４年） ★★ |
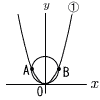 図のように放物線y＝ax2…①と,中心が(0,2)で,原点Oを通る円とが2点A,Bで交わっています。線分ABの長さは4です。(1) aの値を求めなさい。 放物線①上のx＞0の部分に点Cをとると,△ABCの面積は△OABの面積の8倍になりました。 (2) Cの座標を求めなさい。 放物線①上のx＜０の部分に点Dをとると,△OCAの面積と△ODAの面積が等しくなりました。 (3) Dの座標を求めなさい。 (4) 四角形OCDAの面積を求めなさい。 |
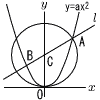 図のように,点C(0,4)を通る直線l が放物線y＝ax2と2点A,Bで交わり,点Aのy座標は6である。点Cを中心とする円が原点０でx軸と接し,点Aを通るとき，(1) 点Aのx座標を求めよ。 (2) 直線l の式を求めよ。 (3) 線分の比AC:CBを求めよ。 (4) 円周上に点Pをとり,△ABPの面積が最大になるようにする。このときの△ABPの面積を求めよ。 |
||
| ２ | 雲雀丘学園高校 （Ｒ４年） ★★★ | ５ | 早大本庄高校 （Ｒ４年） ★★★ |
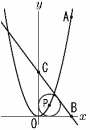 図のように,関数y＝ax2のグラフがあり,点A(4,12)はこのグラフ上にある。また,2点B(4,0),C(0,c)を通る直線BCがあり,直線BCとx軸,y軸に接する円の中心をPとすると,点Pは関数y＝ax2のグラフ上にある。ただし,点Pのx座標は正の数とする。 (1) aの値を求めよ。 (2) 点Pの座標を求めよ。 (3) cの値を求めよ。 |
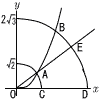 図のように,点Oを原点とする座標平面上に放物線y＝x2と,原点を中心とする半径が√2の円C1と,原点を中心とする半径が2√3の円C2がある。放物線と円C1との交点をA,放物線と円C2の交点をB,円C1とx軸との交点をC,円C2とx軸との交点をD,半直線OAと円C2の交点をEとする。ただし,円周率はπを用いよ。(1) 点Bの座標を求めよ。 (2) 扇形OEBの面積Sを求めよ。 (3) 三角形OBDに内接する円の中心をI とする。点I と円 C上の点との距離dの最小値を求めよ。 |
||
| ３ | 青山学院高等部 （Ｒ６年） ★★ | ６ | 明治大付属中野高校 （Ｒ６年） ★★ |
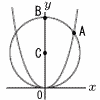 図のように,y軸上の点Cを中心とする原点Oを通る円Cと,関数y＝kx2のグラフがある。円Cとグラフの交点でx座標が正の点をA,円Cとy軸との交点をBとすると,点A,Bのy座標はそれぞれ3a,4aであった。(1) 点Aのx座標とkの値をそれぞれaを用いて表せ。 ∠OBAの二等分線と直線OAの交点をMとする。 (2) 点Mの座標をaを用いて表せ。 (3) △OCM:△OBAを求めよ。 |
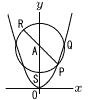 右の図のように,点Ａ(0,8)を中心とする円が放物線y＝ x2と異なる4点で交わっています。そのうちx座標が正である点を,原点に近いほうから順にP,Qとします。また,2点PとAを通る直線と円の交点をR,円とy軸の交点のうち原点に近いほうをＳとします。点Ｑのy座標が8であるとき,(1) 点Pの座標を求めなさい。 (2) 点Sから直線PRに引いた垂線との交点をHとするとき,SHの長さを求めなさい。 |
||
