| ‚Q‚TЃ@•ъ•Ёђь‚ЖҺlЉpЊ`‚Q | Ѓ@Ѓ@Ѓ@ЊҺЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚Q‚TЃ@•ъ•Ёђь‚ЖҺlЉpЊ`‚Q | Ѓ@Ѓ@Ѓ@ЊҺЃ@Ѓ@Ѓ@“ъЃiЃ@Ѓ@Ѓj |
| ‚P | ЉЦђә‘е‘qЉw‰ЂҚ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ | ‚S | –ңҺҰЉw‰@“Њ‘ғҺRҚ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ |
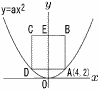 Ѓ@ђ}‚̂悤‚Й,•ъ•ЁђьyЃЃax2Џг‚М2“_A(4,2),D‚р’ё“_‚Ж‚·‚йђі•ыЊ`ABCD‚Ғ‚ ‚йЃB‚Ң‚ң‚µ,“_B‚МyҚА•W‚Нђі‚Е,•У‚`‚a‚НyҺІ‚Й•ҢҚs‚Е‚ ‚йЃB‚Ь‚Ң,•УBC‚ЖyҺІ‚МЊр“_‚рE‚Ж‚·‚йЃB Ѓ@ђ}‚̂悤‚Й,•ъ•ЁђьyЃЃax2Џг‚М2“_A(4,2),D‚р’ё“_‚Ж‚·‚йђі•ыЊ`ABCD‚Ғ‚ ‚йЃB‚Ң‚ң‚µ,“_B‚МyҚА•W‚Нђі‚Е,•У‚`‚a‚НyҺІ‚Й•ҢҚs‚Е‚ ‚йЃB‚Ь‚Ң,•УBC‚ЖyҺІ‚МЊр“_‚рE‚Ж‚·‚йЃB(1) a‚М’l‚р‹Ѓ‚Я‚жЃB (2) •ъ•ЁђьЏг‚Й2“_P,Q‚р‚Ж‚и,P‚МxҚА•W‚Нђі,Q‚МxҚА•W‚Н•‰‚Е‚ ‚й‚Ж‚·‚йЃBҺlЉpЊ`OPEQ‚Ғ‚Р‚µЊ`‚Ж‚И‚й‚Ж‚«‚МP‚МҚА•W‚р‹Ѓ‚Я‚жЃB (3) ђі•ыЊ`ABCD‚МҺь‚М’·‚і‚рl1,–КђП‚рS1‚Ж‚µ,(2)‚М‚Р‚µЊ`OPEQ‚МҺь‚М’·‚і‚рl2,–КђП‚рS2‚Ж‚·‚йЃBl1‚Жl2.S1‚ЖS2‚М‘еЏ¬ЉЦЊW‚Й‚В‚ұ‚Дђі‚µ‚ұ‚а‚М‚р,Һџ‚М‡@Ѓ`‡H‚М‚¤‚ү‚©‚з€к‚В‘I‚ЧЃB Ѓ@Ѓ@‡@l1Ѓѓl2,.S1ЃѓS2Ѓ@‡Al1Ѓѓl2,.S1ЃЃS2Ѓ@‡Bl1Ѓѓl2,.S1Ѓ„S2 Ѓ@Ѓ@‡Cl1ЃЃl2,.S1ЃѓS2Ѓ@‡Dl1ЃЃl2,.S1ЃЃS2Ѓ@‡El1ЃЃl2,.S1Ѓ„S2 Ѓ@Ѓ@‡Fl1Ѓ„l2,.S1ЃѓS2Ѓ@‡Gl1Ѓ„l2,.S1ЃЃS2Ѓ@‡Hl1Ѓ„l2,.S1Ѓ„S2Ѓ@ |
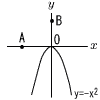 Ѓ@ђ}‚̂悤‚Й,ЉЦђ”yЃЃЃ|x2‚МѓOѓ‰ѓt‚Ж,“_A(Ѓ|2,0),B(0,2)‚Ғ‚ ‚и‚Ь‚·ЃB Ѓ@ђ}‚̂悤‚Й,ЉЦђ”yЃЃЃ|x2‚МѓOѓ‰ѓt‚Ж,“_A(Ѓ|2,0),B(0,2)‚Ғ‚ ‚и‚Ь‚·ЃB(1) ђ}‚М•ъ•ЁђьЏг‚Й2“_C,D‚р‚Ж‚и,ҺlЉpЊ`ABCD‚Ғ•ҢҚsҺl•УЊ`‚Й‚И‚й‚悤‚Й‚µ‚Ь‚·ЃB2“_C,D‚МҚА•W‚р‹Ѓ‚Я‚И‚і‚ұЃB (2) Њө“_‚р’К‚и,(1)‚Е‚Е‚«‚Ң•ҢҚsҺl•УЊ`ABCD‚М–КђП‚р“с“™•Ғ‚·‚й’әђь‚МҺ®‚р‹Ѓ‚Я‚И‚і‚ұЃB (3) (1)‚Е‚Е‚«‚Ң•ҢҚsҺl•УЊ`ABCD‚М–КђП‚р‹Ѓ‚Я‚И‚і‚ұЃB Ѓ@Ѓ@ |
||
| ‚Q | ‘еҚгђҮЊхЉw‰@Қ‚ҚZЃ@Ѓi‚q‚T”NЃjЃ@ЃљЃљЃљ | ‚T | —§–ҢЉЩЊcЏЛҚ‚ҚZЃ@Ѓi‚q‚S”NЃjЃ@ЃљЃљ |
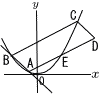 Ѓ@‰E‚Мђ}‚̂悤‚Й,•ъ•ЁђьyЃЃ Ѓ@‰E‚Мђ}‚̂悤‚Й,•ъ•ЁђьyЃЃ(1) “_A‚МxҚА•W‚Н(Ѓ@),“_B‚МxҚА•W‚Н(Ѓ@)‚Е‚ ‚йЃB (2) “_E‚МxҚА•W‚рt‚Е•\‚·‚Ж(Ѓ@Ѓ@)‚Ж‚И‚и,‚µ‚Ң‚Ғ‚Б‚ДtЃЃ(Ѓ@Ѓ@)‚Ж‚И‚йЃB (3) Њө“_O‚р’К‚и,•ҢҚsҺl•УЊ`ABCD‚М–КђП‚р“с“™•Ғ‚·‚й’әђь‚МҺ®‚НyЃЃ(Ѓ@Ѓ@)‚Е‚ ‚йЃB Ѓ@ |
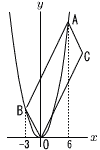 Ѓ@ђ}‚̂悤‚Й,•ъ•ЁђьyЃЃ Ѓ@ђ}‚̂悤‚Й,•ъ•ЁђьyЃЃ(1) “_C‚МҚА•W‚р‹Ѓ‚Я‚И‚і‚ұЃB (2) ’әђьAB‚МҺ®‚р‹Ѓ‚Я‚И‚і‚ұЃB (3) ’әђьAB‚ЖxҺІ‚Ж‚МЊр“_‚рD‚Ж‚·‚йЃB“_D‚р’К‚и,•ҢҚsҺl•УЊ`OCAB‚М–КђП‚р2“™•Ғ‚·‚й’әђь‚МҺ®‚р‹Ѓ‚Я‚И‚і‚ұЃB (4) ђь•ҒABЏг‚Й“_P,xҺІЏг‚ЙxҚА•W‚Ғ10‚Е‚ ‚й“_Q‚р‚Ж‚йЃBЃұOQP‚М–КђП‚Ж•ҢҚsҺl•УЊ`OCAB‚М–КђП‚Ғ“™‚µ‚ұ‚Ж‚«,“_P‚МҚА•W‚р‹Ѓ‚Я‚И‚і‚ұЃB |
||
| ‚R | Њcњд‹`ЏmЏ—ҺqҚ‚ҚZЃ@Ѓi‚q‚U”NЃjЃ@ЃљЃљ | ‚U | ‘Ѓ‘еҚ‚“™Љw‰@Ѓ@Ѓi‚q‚U”NЃjЃ@ЃљЃљЃљ |
Ѓ@•ъ•ЁђьyЃЃx2Џг‚Й3“_‚`(Ѓ|2,4),B(b,b2),C(c,c2)‚Ғ‚ ‚и,Њө“_‚р’К‚иҺlЉpЊ`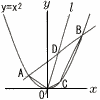 OABC‚М–КђП‚р‚Q“™•Ғ‚·‚й’әђь‚рl ,’әђьAB‚Ж’әђьl ‚МЊр“_‚рD‚Ж‚·‚йЃB’әђьAB‚МЊX‚«‚Н2‚Е,’әђьl ‚МҺ®‚ҒyЃЃ OABC‚М–КђП‚р‚Q“™•Ғ‚·‚й’әђь‚рl ,’әђьAB‚Ж’әђьl ‚МЊр“_‚рD‚Ж‚·‚йЃB’әђьAB‚МЊX‚«‚Н2‚Е,’әђьl ‚МҺ®‚ҒyЃЃ(1) b‚М’l‚р‹Ѓ‚Я‚И‚і‚ұЃB (2) ’әђьABЏг‚Й“_E‚р,ЃұOADЃЃЃұODE‚Ж‚И‚й‚悤‚Й‚Ж‚й‚Ж‚«,“_E‚МxҚА•W‚р‹Ѓ‚Я‚И‚і‚ұЃB‚Ң‚ң‚µ,“_E‚Н“_‚`‚Ж€Щ‚И‚й“_‚Ж‚·‚йЃB (3) c‚М’l‚Ж‚µ‚ДҚl‚¦‚з‚к‚й‚а‚М‚р‚·‚Ч‚Д“љ‚¦‚И‚і‚ұЃB Ѓ@ |
Ѓ@a‚рђі‚М’иђ”‚Ж‚·‚йЃB•ъ•ЁђьyЃЃax2Џг‚Й,4“_A,B,C,D‚Ғ‚ ‚и,“_A,B,C‚МxҚА•W‚Н‚»‚к‚ә‚кЃ|2,Ѓ|1,3‚Е‚ ‚йЃB’әђьAD‚Ж’әђьBC‚Ғ•ҢҚs‚Е‚ ‚й‚Ж‚«, (1) ’әђьBC‚МЊX‚«‚ЖyђШ•Р‚р‚»‚к‚ә‚кa‚МҺ®‚Е•\‚№ЃB (2) “_D‚МxҚА•W‚р‹Ѓ‚Я‚жЃB (3) ҺlЉpЊ`ABCD‚М–КђП‚рa‚МҺ®‚Е•\‚№ЃB (4) ’әђьBC‚ЖyҺІ‚МЊр“_‚р’К‚й’әђь‚Е,ҺlЉpЊ`ABCD‚М–КђП‚р 2“™•Ғ‚·‚й‚а‚М‚МЊX‚«‚рa‚МҺ®‚Е•\‚№ЃB Ѓ@ |
||
ЃmTOPЃnЃmBACKЃnЃmNEXTЃnЃm‰р“љЃnЃ@Ѓ@Ѓљ’† ЃљЃљ‚в‚в“п ЃљЃљЃљ“пЃ@![]() €уҚь—p
€уҚь—p