| ‚Q‚Wپ@چہ•W•½–ت‚R | پ@پ@پ@Œژپ@پ@پ@“ْپiپ@پ@پj |
| ‚Q‚Wپ@چہ•W•½–ت‚R | پ@پ@پ@Œژپ@پ@پ@“ْپiپ@پ@پj |
| ‚P | کa‰جژRŒ§—§چ‚چZپ@پi‚q‚T”Nپjپ@پڑپڑ | ‚S | ‰h–kچ‚چZپ@پi‚q‚T”Nپjپ@پڑ |
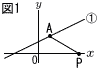 پ@گ}1‚ج‚و‚¤‚ة,ٹضگ”yپپ پ@گ}1‚ج‚و‚¤‚ة,ٹضگ”yپپ(1) پعAPOپپ30پ‹‚ج‚ئ‚«,P‚جxچہ•W‚ً‹پ‚ك‚ب‚³‚¢پB 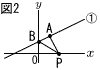 (2) گ}2‚ج‚و‚¤‚ة,‡@‚جƒOƒ‰ƒt‚ئyژ²‚ئ‚جŒً“_‚ًB‚ئ‚·‚éپB‚ـ‚½,yژ²ڈم‚ة“_Q‚ً‚ئ‚è,پ¢ABP‚ئپ¢ABQ‚ج–تگد‚ھ“™‚µ‚‚ب‚é‚و‚¤‚ة‚·‚éپBP‚جxچہ•W‚ھ4‚ج‚ئ‚«,Q‚جچہ•W‚ً‚·‚ׂؤ‹پ‚ك‚ب‚³‚¢پB پ@پ@ |
پ@چہ•W•½–تڈم‚ة2“_A(2,7).B(8.2)‚ھ‚ ‚è‚ـ‚·پBxژ²ڈم‚ج“_P‚ة‚آ‚¢‚ؤ,APپ{PB‚ج’·‚³‚ھ‚à‚ء‚ئ‚à’Z‚‚ب‚é‚ئ‚«‚ج“_P‚جچہ•W‚ً‹پ‚ك‚ب‚³‚¢پB پ@ |
||
| ‚T | گ¼‘هکaٹw‰€چ‚چZپ@پi‚q‚S”Nپjپ@پڑپڑ | ||
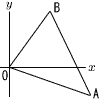 پ@چہ•W•½–تڈم‚ة3“_O(0,0),A(6,پ|2),B(3,4)‚ھ‚ ‚éپBپ¢OAB‚ج–تگد‚ج”¼•ھ‚ھپ¢OAP‚ج–تگد‚ئ“™‚µ‚‚ب‚é‚و‚¤‚ب“_P‚ًyژ²ڈم‚ة‚ئ‚éپBP‚جyچہ•W‚ج’l‚ئ‚µ‚ؤچl‚¦‚¤‚é’l‚ً‚·‚ׂؤ‹پ‚ك‚وپB پ@چہ•W•½–تڈم‚ة3“_O(0,0),A(6,پ|2),B(3,4)‚ھ‚ ‚éپBپ¢OAB‚ج–تگد‚ج”¼•ھ‚ھپ¢OAP‚ج–تگد‚ئ“™‚µ‚‚ب‚é‚و‚¤‚ب“_P‚ًyژ²ڈم‚ة‚ئ‚éپBP‚جyچہ•W‚ج’l‚ئ‚µ‚ؤچl‚¦‚¤‚é’l‚ً‚·‚ׂؤ‹پ‚ك‚وپBپ@ |
|||
| ‚Q | –¾‘ه•t‘®–¾ژ،چ‚چZپ@پi‚q‚S”Nپjپ@پڑپڑپڑ | ‚U | ’}”g‘ه•چ‘®چ‚چZپ@پi‚q‚U”Nپjپ@پڑپڑپڑ |
| پ@چہ•W•½–تڈم‚ة5“_A(پ|2,5),B(پ|5,2),C(پ|3,پ|1),D(1,پ|1),E(4,3)‚ھ‚ ‚éپB“_A‚ً’ت‚è,ŒـٹpŒ`ABCDE‚ج–تگد‚ً2“™•ھ‚·‚é’¼گü‚جژ®‚حyپپ[پ@پ@پ@]‚إ‚ ‚éپB پ@ |
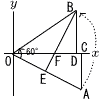 پ@چہ•W•½–ت‚ج“_‚`(8,پ|4)‚ً,Œ´“_O‚ً’†گS‚ئ‚µ‚ؤ”½ژŒv‰ٌ‚è‚ة60پK‚¾‚¯‰ٌ“]‚³‚¹‚½“_‚ً‚a‚ئ‚µ,‚»‚جچہ•W‚ًˆب‰؛‚ج‚و‚¤‚ب•û–@‚إ‹پ‚ك‚邱‚ئ‚ًچl‚¦‚éپB پ@چہ•W•½–ت‚ج“_‚`(8,پ|4)‚ً,Œ´“_O‚ً’†گS‚ئ‚µ‚ؤ”½ژŒv‰ٌ‚è‚ة60پK‚¾‚¯‰ٌ“]‚³‚¹‚½“_‚ً‚a‚ئ‚µ,‚»‚جچہ•W‚ًˆب‰؛‚ج‚و‚¤‚ب•û–@‚إ‹پ‚ك‚邱‚ئ‚ًچl‚¦‚éپBپ@2“_A,B‚©‚çxژ²‚ةگ‚گüAC,BD‚ًˆّ‚پB‚ـ‚½,“_B‚©‚çگü•ھOA‚ةˆّ‚¢‚½گ‚گüBE‚ئxژ²‚ئ‚جŒً“_‚ً‚e‚ئ‚·‚éپB (1) گü•ھOE‚ج’·‚³‚ح,[پ@پ@]‚إ‚ ‚éپB (2) 7“_O,A,B,C,D,E,F‚©‚ç3“_‚ً‘I‚ٌ‚إ‚آ‚‚éژOٹpŒ`‚ج‚¤‚؟, پ¢OAC‚ئ‘ٹژ—‚بژOٹpŒ`‚حپ¢OACˆبٹO‚ة3‚آ‚ ‚è, [پ@پ@], [پ@پ@], پ¢AFE‚إ‚ ‚éپB (3) گü•ھBF‚ج’·‚³‚ح,[پ@پ@]‚إ‚ ‚éپB (4) “_B‚جچہ•W‚ح( [پ@], [پ@] )‚إ‚ ‚éپB پ@ |
||
| ‚R | –¾‘ه•t‘®”ھ‰¤ژqچ‚چZپ@پi‚q‚U”Nپjپ@پڑپڑ | ||
پ@‰E‚جگ}‚ج‚و‚¤‚ة,3“_A(پ|2,2),B(6,18),C(3,0)‚ھ‚ ‚è‚ـ‚·پB’¼گüAO‚ئ’¼گüBC‚جŒً“_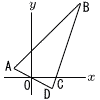 ‚ًD‚ئ‚µ‚ـ‚·پB ‚ًD‚ئ‚µ‚ـ‚·پBپ@ (1) “_B‚ً’ت‚è,پ¢ABD‚ج–تچe‚ً2“™•ھ‚·‚é’¼گü‚جژ®‚ً‹پ‚ك‚ب‚³‚¢پB (2) •سADڈم‚ة“_E‚ً‚ئ‚è‚ـ‚·،پ¢ABE‚ئژlٹpŒ`OABC‚ج–تگد‚ھ“™‚µ‚‚ب‚é‚و‚¤‚ب“_E‚جچہ•W‚ً‹پ‚ك‚ب‚³‚¢پB پ@ |
|||
پmTOPپnپmBACKپnپmNEXTپnپm‰ً“ڑپnپ@پ@پڑ’† پڑپڑ‚â‚â“ï پڑپڑپڑ“ïپ@![]() ˆَچü—p
ˆَچü—p