関数

３０　動点２

月　　　日（　　）

１	盈進高校　（Ｒ４年）　★	４	岐阜県立高校　（Ｒ４年）　★
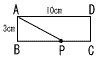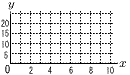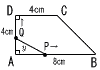点Pは,図のような長方形ABCDの辺BC,CD上を,BからCまでは秒速2cmで動き,CからDまでは秒速1cmで動きます。点PがBを出発してからx秒後の△ABPの面積をycm2とします。 (1) xの変域を求めなさい。 (2) 点PがBからCまで動くとき,yをxの式で表しなさい。 (3) (1)のとき,xとyの関係をグラフに表しなさい。		図のような台形ABCDがある。点P,Qが同時にAを出発して,Pは秒速2cmで台形の辺上をAからBまで動き,Bで折り返してAまで動いて止まり,Qは秒速1cmで台形の辺上をAからDを通ってCまで動いて止まる。P,QがAを出発してからx秒後の△APQの面積をycm2とする。 (1) xの変域が次のとき,yをxの式で表しなさい。 ・0≦x≦4のとき ・4≦x≦8のとき (2) △APQの面積と,台形ABCDから△APQを除いた面積の比が,3:5になるのは,P,QがAを出発してから何秒後と何秒後であるかを求めなさい。
２	ラ・サール高校　（Ｒ４年）　★★★	５	日本大習志野高校　（Ｒ５年）　★★
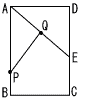図のように,AB＝12,AD＝8の長方形ABCDがあり,辺CDの中点をEとする。2点P,Qは同時にAを出発し,点Pは長方形の辺上をA→B→Cと毎秒2で進み,点Qは線分AE上をA→Eと毎秒１で進む。このとき,出発してからx秒後の△APQの面積をSとして (1) 0≦t≦6のとき,Sをxで表せ。 (2) 6≦t≦10のとき,Sをtで表せ。 (3) △APQの面積が台形ABCEの面積の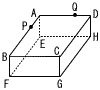になるときのtの値を求めよ。		右図のように,AB＝AD＝18cm,AE＝6cmの直方体ABCD-EFGHがある。2点P,Qは同時に点Aを出発し,点Pは,辺AB上を毎秒2cmの速さで,点Qは,辺AD上を毎秒4cmの速さで往復する。 (1) 出発して初めてAP＝AQとなるのは何秒後か求めなさい。 (2) (1)のとき,立体APQ-EFHの表面積と体積を求めなさい。
３	府立嵯峨野高校　（Ｒ６年）　★★	６	上宮高校　（Ｒ６年）　★★★
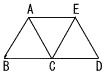図において,△ABC,△ACE,△CDEはいずれも1辺の長さが2cmの正三角形である。点Pは辺AB,BC,CA上を毎秒1cmの速さで点Ａから2点B,Cを通って点Ａまで動く。点Qは辺AC,CD,DE上を毎秒1cmの速さで点Ａから2点C,Dを通って点Eまで動く。6秒後,点Pは点Ａに,点Qは点Eに重なる。 　2点P,Qが同時に出発してからx秒後の△APQの面積をycm2とする。ただし,△ＡPQが存在しないときはy＝０と考えるものとする。 (1) x＝1のとき,yの値を求めよ。 (2) 4≦x≦6のとき,yをxの式で表せ。 (3) yの値が四角形ABDEの面積の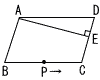となるようなxの値をすべて求めよ。		図のように,AB＝6cm,BC＝9cmの平行四辺形ABCDがあります。点Eは辺CD上の点で,AE⊥CD,DE＝3cmです。点Pはこの平行四辺形の辺上を,点Aを出発してA→B→C→Eの順に点Eまで毎秒2cmの速さで動きます。 (1) 点Pが点Aを出発してから 1秒後の△APEの面積を求めなさい。 (2) AP⊥BCとなるのは,点Pが点Aを出発してから何秒後かを求めなさい。 (3) △APEの面積と平行四辺形ABCDの面積の比が1:3になるときが 2回あります。2回目は,点Pが点Aを出発してから何秒後かを求めなさい。

［TOP］［BACK］［NEXT］［解答］　　★中 ★★やや難 ★★★難　 印刷用