 図形 |
３ 線分比・面積比 | 月 日（ ） |
| 図形 |
３ 線分比・面積比 | 月 日（ ） |
| １ | 香川県立高校 （Ｒ４年） ★★★ | ５ | 京都府立高校 （Ｒ５年） ★ |
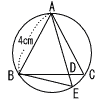 円があり,異なる3点A,B,Cは円周上の点で,△ABCは正三角形である。辺BC上に2点B,Cと異なる点Dをとり,2点A,Dを通る直線と円との交点のうち,点Aと異なる点をEとする。また,点Bと点Eを結ぶ。AB＝4cm,BD:DC＝3:1であるとき,△BDEの面積は何cm2か。 |
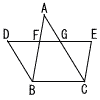 AB‖EC,AC‖DB,DE‖BCである。また,線分DEと線分AB,ACとの交点をそれぞれF,Gとすると,AF:FB=2:3であった。BC=10cmのとき,線分DEの長さを求めよ。 |
||
| ２ | 筑波大附属坂戸高校 （Ｒ４年） ★ | ６ | 筑波大附属駒場高校 （Ｒ５年） ★★★ |
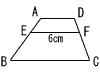 ADとBCが平行でAD:BC=2:5の台形ABCDがあります。辺AB上に,AE:EB =1:2となる点Eをとり,点Eを通って辺BCに平行な直線を引き,辺CDとの交点をFとします。EF＝6cmのとき,BCの長さを答えなさい。 |
AB＝16cm,BC＝(8＋6√2)cm,AC＝2√2cmの△ABCがあります。 点Dは辺AB上にあり,BD＝(8＋4√2)cmです。 点Eは辺BC上にあり,BE＝(√2＋1)cmです。 点Fは辺BC上にあり,CF＝(√2＋1)cmです。 点Gは辺AC上にあり,CG＝(√2−1)cmです。 △ABCの面積をScm2として (1) △ADGの面積を,Sを用いて表しなさい。 (2) △DEGの面積を,Sを用いて表しなさい。 (3) 線分FGの長さを求めなさい。 |
||
| ３ | 日大第三高校 （Ｒ４年） ★★★ | ||
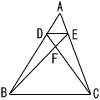 △ABCにおいて,点D,Eをそれぞれ辺AB,AC上にAD:DB＝AE:EC＝1:3となるようにとり,DE＝2cmとする。また,線分BEと線分CDの交点をFとするとき,(1) 辺BCの長さを求めなさい。 (2) BF:FEの比を最も簡単な整数の比で表しなさい。 (3) △BCFの面積は,△ADEの面積の何倍になりますか。 |
|||
| ４ | 慶應義塾志木高校 （Ｒ６年） ★★★ | ７ | 大阪教育大平野校舎 （Ｒ６年） ★★★ |
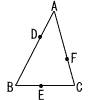 右図の△ABCにおいて,AD:DB＝1:2,BE:EC＝2:3,CF:FA＝3:4である。△ABCの面積をSとするとき,次の図形の面積をSを用いて表せ。(1) 四角形DBCF (2) 線分AEと線分DFの交点をGとするとき,△DEG |
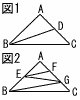 AB＝AC＝10cmの直角二等辺三角形ABCがある。図1は,辺AC上に点Dをとり,線分BDで△ABCの面積を二等分したものである。図2は,辺AB上に点E,辺AC上に点F,Gをとり,線分BG,GE,EFで△ABCの面積を四等分したものである。(1) 線分BDの長さを求めなさい。 (2) 線分FGの長さを求めなさい。 |
||
