 図形 |
１５ 長方形 | 月 日（ ） |
| 図形 |
１５ 長方形 | 月 日（ ） |
| １ | 明大付属中野高校 （Ｒ４年） ★★ | ５ | 愛知県立高校A （Ｒ４年） ★★ |
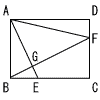 長方形ABCDの辺BC上に点EをBE:EC＝1:2,辺CD上に点FをCF:FD＝3:1となるようにとります。AEとBFの交点をGとします。△AFDの面積が30cm2であるとき,四角形AGFDの面積を求めなさい。 |
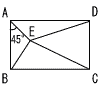 四角形ABCDは長方形であり,Eは長方形ABCDの内部の点で,∠BAE＝45°である。四角形ABCD,△ABE,△AEDの面積がそれぞれ80cm2,10cm2,16cm2のとき, (1) △DCEの面積は何cm2か,求めなさい。 (2) 辺ABの長さは何cmか,求めなさい。 |
||
| ２ | 広島大附属高校 （Ｒ５年） ★★ | ６ | 立命館高校 （Ｒ４年） ★★ |
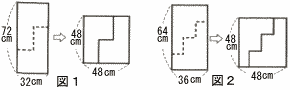 長方形には,図1,図2のように…の線で2つに分割して並べ替えることで,正方形にすることができるものがあります。図1のような切り方を「2段切り」,図2のような切り方を「3段切り」とよぶことにします。縦の長さが128cm,横の長さがxcmの長方形を「7段切り」して正方形にできるとき,xの値を求めなさい。 |
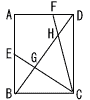 AB＝8cm,BC＝6cmの長方形ABCDにおいて,点Eは辺ABの中点で,点Fは辺DA上にあり,DF:FA＝1:2です。対角線BDと,CEとCFとの交点をそれぞれ点Gと点Hとします。(1) △CGHの面積を求めなさい。 (2) BG:GH:HD＝a:5:bのとき,a,bの値をそれぞれ求めなさい。 (3) 五角形AEGHFの面積を求めなさい。 (4) FH:HG:GE＝c:25:dのとき,c,dの値をそれぞれ求めなさい。 |
||
| ３ | 法政大高校 （Ｒ６年） ★★ | ||
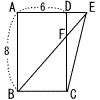 右の図のような長方形ABCDがあり,ADの延長線上に点Eをとり,BEとCDとの交点をFとする。△CEFの面積が8のとき,DEの長さを求めなさい。 |
|||
| ４ | 香川県立高校 （Ｒ６年） ★★ | (1) 線分DFの長さは何cmか。 (2) 四角形ABGEの面積は何cm2か。 |
|
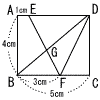 右の図のような,長方形ABCDがある。辺AD上に2点A,Dと異なる点Eをとり,辺BC上に2点B,Cと異なる点Fをとる。線分EFと対角線BDとの交点をGとする。また,点Dと点Fを結ぶ。AB＝4cm,BC＝5cm,AE＝1cm,BF＝3cmであるとき, (右へつづく→) |
|||
